题目内容
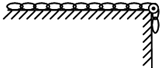 如图所示,一根质量为 m、长为L的匀质链条,一端位于光滑的水平桌面上,另一端少许下垂于桌子边缘,并绕过光滑的定滑轮从静止开始下滑.设桌面足够高,则链条在下滑的过程中,对滑轮产生的最大压力是( )
如图所示,一根质量为 m、长为L的匀质链条,一端位于光滑的水平桌面上,另一端少许下垂于桌子边缘,并绕过光滑的定滑轮从静止开始下滑.设桌面足够高,则链条在下滑的过程中,对滑轮产生的最大压力是( )分析:设链条在定滑轮处的张力为T,压力是F,当链条的垂直部分长度为d时,T最大.根据牛顿第二定律得到链条加速度的表达式和张力T的表达式,运用数学知识求最大值.再运用合成法求压力F.
解答:解:设链条在定滑轮处的张力为T,压力是F,当链条的垂直部分长度为d时,T最大.
链条垂直部分的重力:
F1=
对整个链条,加速度为:a=
=
对链条水平部分:T=
=
由数学知识得:当d=
L,T最大.
解得 Tmax=
mg
Fmax=
=
mg 故B正确.
故选B
链条垂直部分的重力:
F1=
| dmg |
| L |
对整个链条,加速度为:a=
| F1 |
| m |
| dg |
| L |
对链条水平部分:T=
| (L-d)ma |
| L |
| (L-d)dmg |
| L2 |
由数学知识得:当d=
| 1 |
| 2 |
解得 Tmax=
| 1 |
| 4 |
Fmax=
| T |
| cos45° |
| ||
| 4 |
故选B
点评:本题考查运用数学知识解决物理问题的能力,关键要根据牛顿第二定律得到张力的表达式,再求极值.

练习册系列答案
相关题目
 如图所示,一根质量为m的金属棒AC用软线悬挂在磁感强度为B的匀强磁场中,通入A→C方向的电流时,悬线张力不为零,欲使悬线张力为零,可以采用的办法是( )
如图所示,一根质量为m的金属棒AC用软线悬挂在磁感强度为B的匀强磁场中,通入A→C方向的电流时,悬线张力不为零,欲使悬线张力为零,可以采用的办法是( ) 如图所示,一根质量为m的金属棒AC,用软线悬挂在磁感应强度为B的匀强磁场中,电流方向由A→C,此时悬线张力不为零,欲使悬线张力为零,必须( )
如图所示,一根质量为m的金属棒AC,用软线悬挂在磁感应强度为B的匀强磁场中,电流方向由A→C,此时悬线张力不为零,欲使悬线张力为零,必须( ) 如图所示,一根质量为m、长为L的均匀长方体木料放在水平桌面上,木料与桌面间的滑动摩擦力大小为重力的μ倍.现用一水平力F推木料,当木料经过图示位置时,桌面对它的滑动摩擦力大小为
如图所示,一根质量为m、长为L的均匀长方体木料放在水平桌面上,木料与桌面间的滑动摩擦力大小为重力的μ倍.现用一水平力F推木料,当木料经过图示位置时,桌面对它的滑动摩擦力大小为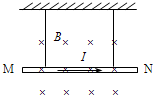 如图所示,一根质量为m的金属棒MN用细线悬挂在磁感应强度为B的匀强磁场中,通入沿M→N方向的电流时,悬线对金属棒的拉力不为零.若要使悬线对棒的拉力为零,可以采用的办法是( )
如图所示,一根质量为m的金属棒MN用细线悬挂在磁感应强度为B的匀强磁场中,通入沿M→N方向的电流时,悬线对金属棒的拉力不为零.若要使悬线对棒的拉力为零,可以采用的办法是( )