题目内容
如图所示,两质量分别为mA和mB的小球A与B套在水平杆CD上,且mA=mB=m,两球之间用一轻细线连接,A和B距转轴O![]() 的距离分别为rA=R,rB=2R,CD对AB的最大静摩擦力都是f,问:
的距离分别为rA=R,rB=2R,CD对AB的最大静摩擦力都是f,问:

(1)要使两球绕轴在水平面内转动而无滑动,角速度ω的最大值?
(2)当ω达到最大值时,绳子受张力为多大?
答案:
解析:
解析:
|
解:当两球绕轴在水平面内转动而无滑动时,设角速度的极大值为ω,由于B球圆周运动的半径较大,需要的向心力较大,则此时两个球有沿水平杆CD向D运动的趋势,设细线上的张力为F,则对A、B分别有牛顿第二定律,有 联立以上两方程,并代入数据求解得 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
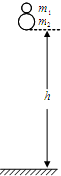 如图所示,两质量分别为m1和m2的弹性小球又叠放在一起,从高度为h处自由落下,且远大于两小球半径,所有的碰撞都是完全弹性碰撞,且都发生在竖直方向.已知m2=3m1,则小球m1反弹后能达到的高度为( )
如图所示,两质量分别为m1和m2的弹性小球又叠放在一起,从高度为h处自由落下,且远大于两小球半径,所有的碰撞都是完全弹性碰撞,且都发生在竖直方向.已知m2=3m1,则小球m1反弹后能达到的高度为( )


