题目内容
如图所示,两平行的光滑金属导轨安装在一光滑绝缘斜面上,导轨间距为l足够长且电阻忽略不计,导轨平面的倾角为α,条形匀强磁场的宽度为d,磁感应强度大小为B、方向与导轨平面垂直.长度为2d的绝缘杆将导体棒和正方形的单匝线框连接在一起组成“![]() ”型装置,总质量为m,置于导轨上.导体棒中通以大小恒为I的电流(由外接恒流源产生,图中未图出).线框的边长为d(d<l),电阻为R,下边与磁场区域上边界重合.将装置由静止释放,导体棒恰好运动到磁场区域下边界处返回,导体棒在整个运动过程中始终与导轨垂直.重力加速度为g.
”型装置,总质量为m,置于导轨上.导体棒中通以大小恒为I的电流(由外接恒流源产生,图中未图出).线框的边长为d(d<l),电阻为R,下边与磁场区域上边界重合.将装置由静止释放,导体棒恰好运动到磁场区域下边界处返回,导体棒在整个运动过程中始终与导轨垂直.重力加速度为g.

求:(1)装置从释放到开始返回的过程中,线框中产生的焦耳热Q;
(2)线框第一次穿越磁场区域所需的时间t1;
(3)经过足够长时间后,线框上边与磁场区域下边界的最大距离xm.
答案:
解析:
解析:
|
(1)设装置由静止释放到导体棒运动到磁场下边界的过程中,作用在线框上的安培力做功为W 由动能定理 且Q=-W 解得 (2)设线框刚离开磁场下边界时的速度为v1,则接着向下运动2d 由动能定理 装置在磁场中运动时收到的合力 感应电动势 感应电流 安培力 由牛顿第二定律,在t到t+ 则 有 解得 (3)经过足够长时间后,线框在磁场下边界与最大距离xm之间往复运动 由动能定理 解得 |

练习册系列答案
相关题目
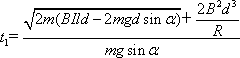
 如图所示,两平行金属板间有一匀强电场,板长为l,板间距离为d,在板右端l处有一竖直放置的光屏M.一带电荷量为q、质量为m的质点从两板中央射入板间,最后垂直打在M屏上,则下列结论正确的是( )
如图所示,两平行金属板间有一匀强电场,板长为l,板间距离为d,在板右端l处有一竖直放置的光屏M.一带电荷量为q、质量为m的质点从两板中央射入板间,最后垂直打在M屏上,则下列结论正确的是( ) 如图所示,两平行金属板间有一匀强电场,板长为L,板间距离为d,在板右端L处有一竖直放置的光屏M,一带电荷量为q,质量为m的质点从两板中央射入板间,最后垂直打在M屏上,则下列结论正确的是( )
如图所示,两平行金属板间有一匀强电场,板长为L,板间距离为d,在板右端L处有一竖直放置的光屏M,一带电荷量为q,质量为m的质点从两板中央射入板间,最后垂直打在M屏上,则下列结论正确的是( ) 如图所示,两平行金属板间有一匀强电场,板长为L,板间距离为d,在 板右端L处有一竖直放置的光屏M,一带电荷量为q,质量为m的质点从两板中央射入板间,最后垂直打在M屏上,则下列结论正确的是( )
如图所示,两平行金属板间有一匀强电场,板长为L,板间距离为d,在 板右端L处有一竖直放置的光屏M,一带电荷量为q,质量为m的质点从两板中央射入板间,最后垂直打在M屏上,则下列结论正确的是( ) (2012?邯郸模拟)如图所示,两面平行的玻璃砖下表面涂有反射物质,一束与上表面成30°入射的光线,在右端垂直标尺上形成了A、B两个光斑,A、B间距为4cm,已知玻璃砖的折射率为
(2012?邯郸模拟)如图所示,两面平行的玻璃砖下表面涂有反射物质,一束与上表面成30°入射的光线,在右端垂直标尺上形成了A、B两个光斑,A、B间距为4cm,已知玻璃砖的折射率为