题目内容
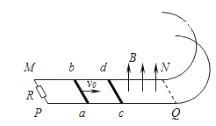
【题目】如图所示为依据回旋加速器原理设计的一个小型粒子加速器的原理示意图，区域Ⅰ和区域Ⅱ分别存在匀强磁场B1和B2。在宽度为L的区域Ⅲ内存在一个水平方向的匀强电场E，通过调整方向使进入区域Ⅲ的粒子持续加速。在图中A位置有一个带正电的粒子由静止释放，粒子经过两次电场加速后最终垂直区域Ⅰ的边缘AE射出(粒子质量为m，带电量为q，不计重力和阻力)。求：
(1)粒子进入区域Ⅰ和区域Ⅱ的速度之比；
(2)区域Ⅰ和区域Ⅱ的磁场强度之比；
(3)已知区域Ⅰ的场强B1＝B，求从粒子释放到区域Ⅰ边缘飞出的总时间。
【答案】(1)
∶1 (2)1∶ (3)
【解析】
(1)由题意作出粒子运动的轨迹如图所示：
带电粒子由静止释放，在电场中加速进入区域Ⅱ，经过半个圆周的偏转进入区域Ⅲ继续加速，进入区域Ⅰ经过
圆周偏转垂直边缘AE射出。粒子进入区域Ⅰ时经历了两次电场加速，
2EqL＝
mvⅠ2
粒子进入区域Ⅱ时经历了一次电场加速，
EqL＝mvⅡ2
联立可得
vⅠ∶vⅡ＝∶1
(2)根据题意，带电粒子在区域Ⅰ和区域Ⅱ中的圆周轨迹半径之比
＝
根据向心力表达式：
＝Bqv
得
B＝
将半径代入可得
BⅠ∶BⅡ＝1∶
(3)带电粒子在三个区域运动时间设为tⅠ、tⅡ、tⅢ，粒子在匀强磁场中运动的周期为
T＝
BⅠ＝B，BⅡ＝B
粒子在匀强磁场区域Ⅰ中运动的时间
tⅠ＝TⅠ＝
，
粒子在匀强磁场区域Ⅱ中运动的时间
tⅡ＝TⅡ＝
，
粒子在电场区域Ⅲ中加速，电场为F＝Eq，总距离是2L，
根据匀变速直线运动规律得：
2L＝atⅢ2，a＝
，
联立得
tⅢ＝2
总时间为
t＝tⅠ＋tⅡ＋tⅢ＝
＋2
练习册系列答案
相关题目
