题目内容
【题目】如图所示，光滑杆AB长为L，B端固定一根劲度系数为k、原长为l0的轻弹簧，质量为m的小球套在光滑杆上并与弹簧的上端连接， 
为过B点的竖直轴，杆与水平面间的夹角始终为
。
⑴杆保持静止状态时小球对弹簧的压缩量
；
⑵当球随杆一起绕
轴匀速转动时，弹簧伸长量为
，求匀速转动的角速度
。
【答案】⑴
⑵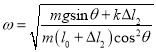
【解析】试题分析：小球从弹簧的原长位置静止释放时，根据牛顿第二定律求解加速度，小球速度最大时其加速度为零，根据合力为零和胡克定律求解
；（2）设弹簧伸长
时，对小球受力分析，根据向心力公式列式求解．
（1）小球释放瞬间，加速度为
当小球速度最大时，有
解得弹簧的压缩量为
（2）对小球受力分析，建立坐标系，
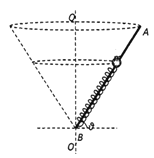
水平方向上： 
竖直方向有： 
—
=mg
解得： 
练习册系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
