题目内容
6.“嫦娥二号”新开辟了地月之间的“直航航线”,即直接发射至地月转移轨道,再进入距月面约h的圆形工作轨道,开始进行科学探测活动.设月球半径为R,月球表面的重力加速度为g月,万有引力常量为G,则下列说法正确的是( )| A. | 由题目条件可知月球的平均密度为$\frac{{3{g_月}}}{4πGR}$ | |
| B. | “嫦娥二号”在工作轨道上绕月球运行的周期为$2π\sqrt{\frac{R}{g_月}}$ | |
| C. | “嫦娥二号”在工作轨道上的绕行速度为$\sqrt{{g_月}(R+h)}$ | |
| D. | “嫦娥二号”在工作轨道上运行时的向心加速度为($\frac{R}{R+h}$)2g月 |
分析 月球表面重力等于万有引力,绕月卫星的向心力由万有引力提供,据此列式分析即可.
解答 解:A、在月球表面重力与万有引力相等有可得月球质量M=$\frac{{{g_月}{R^2}}}{G}$,据密度公式可得月球密度$\frac{{3{g_月}}}{4πGR}$,故A正确;
B、根据万有引力提供圆周运动向心力有可得周期
T=$2π\sqrt{\frac{{(R+h{)^3}}}{GM}}$=$2π\sqrt{\frac{{(R+h{)^3}}}{{{g_月}{R^2}}}}$,故B错误;
C、根据万有引力提供圆周运动向心力可得嫦娥二号绕行速度为$\sqrt{\frac{{g{R^2}}}{R+h}}$,故C错误;
D、根据万有引力提供圆周运动向心力可得嫦娥二号在工作轨道上的向心加速度,故D正确.
故选:AD.
点评 解决本题的关键是抓住星球表面重力与万有引力相等,万有引力提供圆周运动向心力入手,掌握公式及公式变换是正确解题的关键.

练习册系列答案
相关题目
17.关于曲线运动,下列说法正确的是( )
| A. | 做曲线运动物体的速度方向可以不变 | |
| B. | 曲线运动一定是变速运动 | |
| C. | 物体受到变力作用时就做曲线运动 | |
| D. | 物体做圆周运动,所受的合力一定指向圆心 |
14.关于运动的合成,下列说法正确的是( )
| A. | 两个匀速直线运动的合运动一定是匀速直线运动 | |
| B. | 一个匀速直线运动和一个匀加速直线运动的合运动一定是曲线运动 | |
| C. | 两个加速度不等的匀加速直线运动的合运动可能是匀变速曲线运动 | |
| D. | 两个加速度不等的匀加速直线运动的合运动不可能是匀变速直线运动 |
18.如图甲所示用极微弱的黄光做双缝干涉实验,随着时间的增加,在屏上先后出现如图(a)、(b)、(c)所示的图象.如图乙所示是两列完全相同的相干水波在某时刻的叠加情况,图中实线表示波峰,虚线表示波谷.则( )


| A. | 甲图中图象(a)表明光具有粒子性,图象(c)表明光具有波动性 | |
| B. | 改用红光观察现象和图中是一样的 | |
| C. | 实验表明光是一种概率波 | |
| D. | 乙图中从该时刻起,经过四分之一个周期,质点M将到达平衡位置,位移为零 | |
| E. | 乙图中OM连线的中点是振动加强点,其振幅为单个波引起的振幅的2倍 |
 如图所示,匀强电场的宽度为d,电子以速率为v0沿垂直于场强方向穿越匀强电场,偏角θ=60°,电子的电荷量为-e,质量为m.求:
如图所示,匀强电场的宽度为d,电子以速率为v0沿垂直于场强方向穿越匀强电场,偏角θ=60°,电子的电荷量为-e,质量为m.求: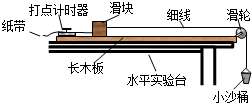 某探究学习小组同学欲验证“动能定理”,他们在实验室组装了一套如图所示的装置,另外还找到了打点计时器所用的学生电源、导线、复写纸、纸带、小木块、细沙、天平、刻度尺.当滑块连接上纸带,用细线通过滑轮挂上空的小沙桶时,释放小桶,滑块处于静止状态.
某探究学习小组同学欲验证“动能定理”,他们在实验室组装了一套如图所示的装置,另外还找到了打点计时器所用的学生电源、导线、复写纸、纸带、小木块、细沙、天平、刻度尺.当滑块连接上纸带,用细线通过滑轮挂上空的小沙桶时,释放小桶,滑块处于静止状态.
 如图甲所示,固定在水平桌边上的L双轨型平行金属导轨足够长,倾角为θ=53°,间距L=2m,电阻不计;导轨上两根金属棒ab、cd的阻值分别为R1=25Ω,R2=4Ω,ab棒的质量m1=5.0kg,cd棒质量m2=1.0kg,ab与导轨间的动摩擦因数μ1=$\frac{2}{15}$,cd与导轨间的动摩擦因数μ2=0.5,设最大静摩擦力等于滑动摩擦力,整个导轨置于磁感应强度B=5T、方向垂直倾斜导轨平面向上的匀强磁场中.现让ab棒从导轨上离桌面某一高度处由静止释放,当它刚要滑出导轨时,cd棒也恰好开始滑动,且ab棒下滑阶段,通过ab棒的电荷量为q=2C;g取10m/s2.求
如图甲所示,固定在水平桌边上的L双轨型平行金属导轨足够长,倾角为θ=53°,间距L=2m,电阻不计;导轨上两根金属棒ab、cd的阻值分别为R1=25Ω,R2=4Ω,ab棒的质量m1=5.0kg,cd棒质量m2=1.0kg,ab与导轨间的动摩擦因数μ1=$\frac{2}{15}$,cd与导轨间的动摩擦因数μ2=0.5,设最大静摩擦力等于滑动摩擦力,整个导轨置于磁感应强度B=5T、方向垂直倾斜导轨平面向上的匀强磁场中.现让ab棒从导轨上离桌面某一高度处由静止释放,当它刚要滑出导轨时,cd棒也恰好开始滑动,且ab棒下滑阶段,通过ab棒的电荷量为q=2C;g取10m/s2.求