题目内容
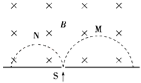
【题目】如图所示，一质量为m，带电量为－q，不计重力的粒子，从x轴上的P(a,0)点以速度大小为v，沿与x轴正方向成60°的方向射入第一象限内的匀强磁场中，并恰好垂直于y轴射出第一象限。求：
(1)匀强磁场的磁感应强度B；
(2)穿过第一象限的时间t。
【答案】
,
【解析】解：（1）设磁感应强度为B，粒子在磁场中做匀速圆周运动的半径为r．粒子在磁场中做匀速圆周运动，洛仑兹力提供向心力，由牛顿第二定律得：
qvB=m
…①，
粒子运动轨迹如图所示，由几何知识得：r=
…②
由①②解得：B=
…③；
（2）设粒子在磁场中做匀速圆周运动的周期为T，则T=
…④
由图知，粒子在磁场中做圆周运动对应的圆心角为：θ=
…⑤
粒子在磁场中运动的时间为：t=
T…⑥
由②④⑤⑥解得：t=
；
答：匀强磁场的磁感应强度B为
，带电粒子在磁场中的运动时间是．
练习册系列答案
同步练习强化拓展系列答案
相关题目
