题目内容
如图所示，一个带电粒子从粒子源飘入（初速度很小，可忽略不计）电压为U1的加速电场，经加速后从小孔S沿平行金属板A、B的中心线射入，A、B板长为L，相距为d，电压为U2，则带电粒子能从A、B板间飞出应该满足的条件是（不计粒子重力）（ ）
A．
＜
B．
＜
C．
＜
D．
＜
【答案】分析：带电粒子无初速度在加速电场中被加速，又以一定速度垂直进入偏转电场，由于速度与电场力垂直，所以粒子先做匀加速直线运动，后做类平抛运动．这样类平抛运动可将看成沿初速度方向的匀速直线与垂直于初速度方向匀加速直线运动．可利用加速电场的电压U求出进入偏转电场的初速度，然后运用偏转电场的长度L求出运动时间，由于分运动间具有等时性，所以由运动学公式求出垂直于初速度方向的位移．值得注意的是，求出的位移不是等于偏转电场的宽度，而是小于或等于宽度的一半．
解答：解：带电粒子在电场中被加速，
则有 qu1=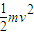
-0 （1）
带电粒子在偏转电场中做类平抛运动，可看成匀速直线运动与匀加速直线运动的两分运动．
匀速直线运动：由运动学公式得 L=vt （2）
匀加速直线运动：设位移为x，则有x=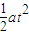
=
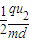t2 （3）
要使带电粒子能飞出电场，则有x＜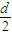
（4）
由（1）-（4）可得：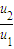
＜
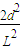
故选：C．
点评：考查带电粒子在电场中加速与偏转，从而先做匀加速直线运动，后做匀加速曲线运动．运用了运动学公式与动能定理，同时体现出处理类平抛运动的方法．还值得注意是：粒子的偏转位移应小于偏转电场宽度的一半．
解答：解：带电粒子在电场中被加速，
则有 qu1=
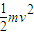-0 （1）带电粒子在偏转电场中做类平抛运动，可看成匀速直线运动与匀加速直线运动的两分运动．
匀速直线运动：由运动学公式得 L=vt （2）
匀加速直线运动：设位移为x，则有x=
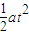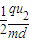=t2 （3）要使带电粒子能飞出电场，则有x＜
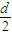（4）由（1）-（4）可得：
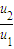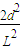
＜故选：C．
点评：考查带电粒子在电场中加速与偏转，从而先做匀加速直线运动，后做匀加速曲线运动．运用了运动学公式与动能定理，同时体现出处理类平抛运动的方法．还值得注意是：粒子的偏转位移应小于偏转电场宽度的一半．
练习册系列答案
学而优暑期衔接南京大学出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
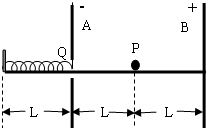如图所示，A、B是两块竖直放置的平行金属板，相距为2L，分别带有等量的负、正电荷，在两板间形成电场强度大小为E的匀强电场．A板上有一小孔（它的存在对两板间匀强电场分布的影响可忽略不计），孔的下沿右侧有一条与板垂直的水平光滑绝缘轨道，一个质量为m，电荷量为g（g＞0）的小球（可视为质点），在外力作用下静止在轨道的中点P处．孔的下沿左侧也有一与板垂直的水平光滑绝缘轨道，轨道上距A板L处有一固定档板，长为L的轻弹簧左端固定在挡板上，右端固定一块轻小的绝缘材料制成的薄板Q．撤去外力释放带电小粒，它将在电场力作用下由静止开始向左运动，穿过小孔后（不与金属板A接触）与薄板Q一起压缩弹簧，由于薄板Q及弹簧的质量都可以忽略不计，可认为小球与Q接触过程中不损失机械能．小球从接触Q开始，经历时间To第一次把弹簧压缩至最短，然后又被弹簧弹回．由于薄板Q的绝缘性能有所欠缺，使得小球每次离开Q瞬间，小球的电荷量都损失一部分，而变成刚与Q接触时小球电荷量的
（2006?奉贤区模拟）如图所示，平行金属板内有一匀强电场，一个电量为q、质量为m的带电粒子（重力不计）以速度v0从A点水平射人电场，且刚好以速度v从B点射出，则（ ）
在研究性学习中，某同学设计了一个测定带电粒子 比荷的实验，其实验装置如图所示．abcd 是一个长方形盒子，在 ad 边和 cd 边上各开有小孔f和e，e 是 cd 边上的中点，荧光屏 M 贴着cd放置，能显示从 e 孔射出的粒 子落点位置．盒子内有一方向垂直于 abcd 平面的匀强磁场，磁感应强度大小为 B．粒子源不断地发射相同的带电粒子，粒子的初速度可以忽略．粒子经过电压为U的电场加速后，从 f 孔垂直于 ad 边射入盒内．粒子经磁场偏转后恰好从e孔射出．若已知 fd=cd=L，不计粒子的重力和粒子之间的相互作用力．求：
如图所示，一个质量为m的带正电量为q的尘粒，以竖直向上的初速
在平行板电容器PQ两板正中间的A点进入场强为E的匀强电场中，恰好垂直于Q板打在B点，且
，则下列说法正确的是（ ）
，电荷量为
的小球（可视为质点）， 在外力作用下静止在轨道的中点P处。孔的下沿左侧也有一与板垂直的水平光滑绝缘轨道，轨道上距A板L处有一固定档板，长为L的轻弹簧左端固定在挡板上，右端固定一块轻小的绝缘材料制成的薄板Q。撤去外力释放带电小粒，它将在电场力作用下由静止开始向左运动，穿过小孔后（不与金属板A接触）与薄板Q一起压缩弹簧，由于薄板Q及弹簧的质量都可以忽略不计，可认为小球与Q接触过程中不损失机械能。小球从接触 Q开始，经历时间T0第一次把弹簧压缩至最短，然后又被弹簧弹回。由于薄板Q的绝缘性能有所欠缺，使得小球每次离开Q瞬间，小球的电荷量都损失一部分，而变成刚与Q接触时小球电荷量的
。求：
次弹回两板间后向右运动的最远处没有到达B板，试导出小球从第
，且小孔右侧的轨道粗糙与带电小球间的滑动摩擦力为
，试求带电小球最终停止的位置距P点的距离。