Question

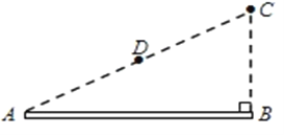
【题目】如图所示，平行板电容器的两极板、与水平地面成角，电势差为。建立平面直角坐标系，电容器极板边缘无限靠近坐标原点，在（，）处是一垂直轴的荧光屏。在区域有竖直向上的匀强电场，场强，在平面内以（，）点为圆心，半径为的圆形区域内有垂直于纸面向里的匀强磁场，磁感应强度，一质量，电量的带电粒子，从A（，0）点（即电容器两极板间距离的中点）由静止开始运动，它能沿轴作直线运动，到达坐标原点后进入电磁复合场，粒子最终打在荧光屏上点，,,，

（1）求两极板间电势差以及极板电性；

（2）粒子到达坐标原点O时的速度；

（3）粒子从A点到N点所用时间（该问结果保留一位有效数字）。

Answer 1

【答案】（1）0.04V；P板带负电（2）1m/s（3）0.4s

【解析】

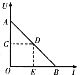
（1）粒子在电容器间做匀加速直线运动，受力分析如图所示，可得：

根据几何关系得：

联立解得：

粒子过磁场向上偏转，故带正电，粒子在电容器中受力指向板，故板带负电

（2）粒子在电容器中，由牛顿第二定律得：

解得粒子加速度

由运动学公式得：

（3）粒子在电磁复合场中静电力：

与重力平衡，粒子先在磁场中做匀速圆周运动，离开磁场后做匀速直线运动打到N点，如图所示，

根据牛顿第二定律和向心力公式得

圆周运动半径：

可得：

所以：

故

粒子做圆周运动时间为：

从到用时：

故粒子从点到点所用时间：

。