题目内容
 如图所示,一个带电粒子以大小为vA的水平速度从A点垂直电场线射入场强大小为E的匀强电场,经过电场中B点时速度大小为vB,AB间水平距离为d,不计重力和空气阻力.则由上述四个已知量可以求得以下的未知量,它们是( )
如图所示,一个带电粒子以大小为vA的水平速度从A点垂直电场线射入场强大小为E的匀强电场,经过电场中B点时速度大小为vB,AB间水平距离为d,不计重力和空气阻力.则由上述四个已知量可以求得以下的未知量,它们是( )| A、带电粒子电量与质量的比值 | B、带电粒子在A、B两点电势能之差 | C、速度vB的方向 | D、A、B两点间的电势差 |
分析:带电粒子垂直进入电场中做类平抛运动,水平方向做匀速直线运动,竖直方向做初速度为0的匀加速直线运动,由牛顿第二定律得到竖直分速度的表达式;根据动能定理列式;速度vB的方向的反向延长线通过水平位移的中点;根据这些知识和表达式进行分析.
解答:解:A、带电粒子在电场中做类平抛运动,根据速度的分解可知:经过B点时竖直方向的分速度大小为:vy=
;
根据牛顿第二定律和运动学公式得:a=
,vy=at,t=
联立以上四式得
=
,vA、vB、E、d均已知,则可求得
.故A正确.
B、根据能量守恒得:带电粒子在A、B两点电势能之差△Ep=
m
-
m
,因m不能求出,则△Ep不能求出.故B错误.
C、设速度vB与水平方向的夹角为α,则tanα=
,可知α可以解出,故C正确.
D、根据动能定理得:qUAB=
m
-
m
,因可求得
,vA、vB均已知,则可求出UAB.故D正确.
故选:ACD
|
根据牛顿第二定律和运动学公式得:a=
| qE |
| m |
| d |
| vA |
联立以上四式得
|
| qEd |
| mvA |
| q |
| m |
B、根据能量守恒得:带电粒子在A、B两点电势能之差△Ep=
| 1 |
| 2 |
| v | 2 B |
| 1 |
| 2 |
| v | 2 A |
C、设速度vB与水平方向的夹角为α,则tanα=
| vy |
| vA |
D、根据动能定理得:qUAB=
| 1 |
| 2 |
| v | 2 B |
| 1 |
| 2 |
| v | 2 A |
| q |
| m |
故选:ACD
点评:本题中带电粒子垂直进入匀强电场做类平抛运动,采用运动的分解研究,根据牛顿第二定律和运动学公式、动能定理得到表达式,再进行分析,是常用的方法和思路.

练习册系列答案
相关题目
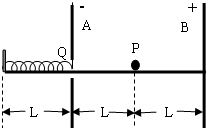 如图所示,A、B是两块竖直放置的平行金属板,相距为2L,分别带有等量的负、正电荷,在两板间形成电场强度大小为E的匀强电场.A板上有一小孔(它的存在对两板间匀强电场分布的影响可忽略不计),孔的下沿右侧有一条与板垂直的水平光滑绝缘轨道,一个质量为m,电荷量为g(g>0)的小球(可视为质点),在外力作用下静止在轨道的中点P处.孔的下沿左侧也有一与板垂直的水平光滑绝缘轨道,轨道上距A板L处有一固定档板,长为L的轻弹簧左端固定在挡板上,右端固定一块轻小的绝缘材料制成的薄板Q.撤去外力释放带电小粒,它将在电场力作用下由静止开始向左运动,穿过小孔后(不与金属板A接触)与薄板Q一起压缩弹簧,由于薄板Q及弹簧的质量都可以忽略不计,可认为小球与Q接触过程中不损失机械能.小球从接触Q开始,经历时间To第一次把弹簧压缩至最短,然后又被弹簧弹回.由于薄板Q的绝缘性能有所欠缺,使得小球每次离开Q瞬间,小球的电荷量都损失一部分,而变成刚与Q接触时小球电荷量的
如图所示,A、B是两块竖直放置的平行金属板,相距为2L,分别带有等量的负、正电荷,在两板间形成电场强度大小为E的匀强电场.A板上有一小孔(它的存在对两板间匀强电场分布的影响可忽略不计),孔的下沿右侧有一条与板垂直的水平光滑绝缘轨道,一个质量为m,电荷量为g(g>0)的小球(可视为质点),在外力作用下静止在轨道的中点P处.孔的下沿左侧也有一与板垂直的水平光滑绝缘轨道,轨道上距A板L处有一固定档板,长为L的轻弹簧左端固定在挡板上,右端固定一块轻小的绝缘材料制成的薄板Q.撤去外力释放带电小粒,它将在电场力作用下由静止开始向左运动,穿过小孔后(不与金属板A接触)与薄板Q一起压缩弹簧,由于薄板Q及弹簧的质量都可以忽略不计,可认为小球与Q接触过程中不损失机械能.小球从接触Q开始,经历时间To第一次把弹簧压缩至最短,然后又被弹簧弹回.由于薄板Q的绝缘性能有所欠缺,使得小球每次离开Q瞬间,小球的电荷量都损失一部分,而变成刚与Q接触时小球电荷量的 (2006?奉贤区模拟)如图所示,平行金属板内有一匀强电场,一个电量为q、质量为m的带电粒子(重力不计)以速度v0从A点水平射人电场,且刚好以速度v从B点射出,则( )
(2006?奉贤区模拟)如图所示,平行金属板内有一匀强电场,一个电量为q、质量为m的带电粒子(重力不计)以速度v0从A点水平射人电场,且刚好以速度v从B点射出,则( ) 在研究性学习中,某同学设计了一个测定带电粒子 比荷的实验,其实验装置如图所示.abcd 是一个长方形盒子,在 ad 边和 cd 边上各开有小孔f和e,e 是 cd 边上的中点,荧光屏 M 贴着cd放置,能显示从 e 孔射出的粒 子落点位置.盒子内有一方向垂直于 abcd 平面的匀强磁场,磁感应强度大小为 B.粒子源不断地发射相同的带电粒子,粒子的初速度可以忽略.粒子经过电压为U的电场加速后,从 f 孔垂直于 ad 边射入盒内.粒子经磁场偏转后恰好从e孔射出.若已知 fd=cd=L,不计粒子的重力和粒子之间的相互作用力.求:
在研究性学习中,某同学设计了一个测定带电粒子 比荷的实验,其实验装置如图所示.abcd 是一个长方形盒子,在 ad 边和 cd 边上各开有小孔f和e,e 是 cd 边上的中点,荧光屏 M 贴着cd放置,能显示从 e 孔射出的粒 子落点位置.盒子内有一方向垂直于 abcd 平面的匀强磁场,磁感应强度大小为 B.粒子源不断地发射相同的带电粒子,粒子的初速度可以忽略.粒子经过电压为U的电场加速后,从 f 孔垂直于 ad 边射入盒内.粒子经磁场偏转后恰好从e孔射出.若已知 fd=cd=L,不计粒子的重力和粒子之间的相互作用力.求: 如图所示,一个质量为m的带正电量为q的尘粒,以竖直向上的初速
如图所示,一个质量为m的带正电量为q的尘粒,以竖直向上的初速