Question

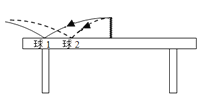
【题目】如图甲所示是游乐场中过山车的实物图片，可将过山车的一部分运动简化为图18乙的模型图，此模型中所有轨道都是光滑的。现使小车（视作质点）从左侧轨道距B点高h=0.25m处（图中未标出）由静止开始向下运动，B点为圆轨道的最低点，小车进入圆轨道后，恰好能通过轨道的最高点A处。不计空气阻力，小车的质量m=1.0kg，g取10m/s2。求：

（1）小车通过B点时的速度大小vB；

（2）圆轨道的半径R的大小；

（3）小车通过到圆轨道B点时对轨道的压力大小FB。

Answer 1

【答案】（1）m/s（2）R=0.1m（3）60N

【解析】（1）由动能定理，有

得m/s

（2）设小车经过A点时的速度为vA，根据牛顿第二定律有

得vA=

依据机械能守恒定律，有

得

结合（1）可得 R=0.1m

（3）设轨道在最低点给小车的支持力为FB′，根据牛顿第二定律有

FB′mg =

解得FB′=60N

由第牛顿三定律可知，球对轨道的作用力FB=60N