题目内容
 如图所示,在电场强度E=104N/C的水平匀强电场中,有一根长l=15cm的细线,一端固定在O点,另一端系在一个质量为m=3g,带电荷量q=2×10-6C的小球,当细线处于水平位置时,小球从静止开始释放,求小球到达最低点B时对细线的拉力.
如图所示,在电场强度E=104N/C的水平匀强电场中,有一根长l=15cm的细线,一端固定在O点,另一端系在一个质量为m=3g,带电荷量q=2×10-6C的小球,当细线处于水平位置时,小球从静止开始释放,求小球到达最低点B时对细线的拉力.分析:小球由最高点到最低点有重力和电场力做功,由动能定理可求得小球在最低点的速度.
小球经过最低点时,由重力的细线的拉力的合力提供向心力,根据牛顿第二定律求解细线的拉力,再根据牛顿第三定律得到小球对细线的拉力.
小球经过最低点时,由重力的细线的拉力的合力提供向心力,根据牛顿第二定律求解细线的拉力,再根据牛顿第三定律得到小球对细线的拉力.
解答:解:从A到B过程,由动能定理:mgl-qEl=
mv2
在最低点,设绳子对小球的拉力为F,则有根据牛顿第二定律得:
F-mg=m
联立解得:F=5×10-2N
由牛顿第三定律,小球对绳子的拉力与绳子对小球的拉力是一对相互作用力
所以小球对绳子的拉力为5×10-2N.
答:小球到达最低点B时对细线的拉力是5×10-2N.
| 1 |
| 2 |
在最低点,设绳子对小球的拉力为F,则有根据牛顿第二定律得:
F-mg=m
| v2 |
| l |
联立解得:F=5×10-2N
由牛顿第三定律,小球对绳子的拉力与绳子对小球的拉力是一对相互作用力
所以小球对绳子的拉力为5×10-2N.
答:小球到达最低点B时对细线的拉力是5×10-2N.
点评:带电物体在电场中的运动若不涉及时间时,动能定理是最佳解题选择.对于圆周运动,确定向心力的来源是求解的关键.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
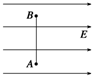 如图所示,在电场强度为E、方向水平向右的匀强电场中,A、B为一竖直线上的两点,相距为L,外力F将质量为m、带电荷量为q的粒子从A点匀速移到B点,重力不能忽略,则下列说法中正确的是( )
如图所示,在电场强度为E、方向水平向右的匀强电场中,A、B为一竖直线上的两点,相距为L,外力F将质量为m、带电荷量为q的粒子从A点匀速移到B点,重力不能忽略,则下列说法中正确的是( )| A、外力的方向水平向左 | ||
| B、外力的方向竖直向上 | ||
| C、外力的大小等于qE+mg | ||
D、外力的大小等于
|
 如图所示,在电场强度为E的水平匀强电场中,有一长为L,质量可以忽略不计的绝缘杆,可绕通过杆中点并与电场强度方向垂直的水平轴O在竖直平面内转动(轴间摩擦不计).杆的两端各固定一个小球A和B,它们的质量分别为2m和m,电量分别为2Q和-Q.开始时,杆处在图中所示的竖直位置,然后放手,杆发生转动,求杆转过900到达水平位置时A球的动能.
如图所示,在电场强度为E的水平匀强电场中,有一长为L,质量可以忽略不计的绝缘杆,可绕通过杆中点并与电场强度方向垂直的水平轴O在竖直平面内转动(轴间摩擦不计).杆的两端各固定一个小球A和B,它们的质量分别为2m和m,电量分别为2Q和-Q.开始时,杆处在图中所示的竖直位置,然后放手,杆发生转动,求杆转过900到达水平位置时A球的动能. (2012?通州区模拟)如图所示,在电场强度为E的匀强电场中,一个电荷量为q的正点电荷,沿电场线方向从A点运动到B点,A、B两点间的距离为d.在此过程中电场力对电荷做的功等于( )
(2012?通州区模拟)如图所示,在电场强度为E的匀强电场中,一个电荷量为q的正点电荷,沿电场线方向从A点运动到B点,A、B两点间的距离为d.在此过程中电场力对电荷做的功等于( ) (2010?黑龙江模拟)如图所示,在电场强度为2.0×102V/m的匀强电场中,A、B两点相距0.30m,则A、B两点间的电势差为
(2010?黑龙江模拟)如图所示,在电场强度为2.0×102V/m的匀强电场中,A、B两点相距0.30m,则A、B两点间的电势差为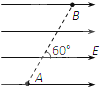 如图所示,在电场强度E=5×105V/m的匀强电场中,将一电荷量q=2×10-5C的正电荷由A点移到B点,已知A、B两点间距离为2cm,两点连线与电场方向成60°角,求:
如图所示,在电场强度E=5×105V/m的匀强电场中,将一电荷量q=2×10-5C的正电荷由A点移到B点,已知A、B两点间距离为2cm,两点连线与电场方向成60°角,求: