题目内容
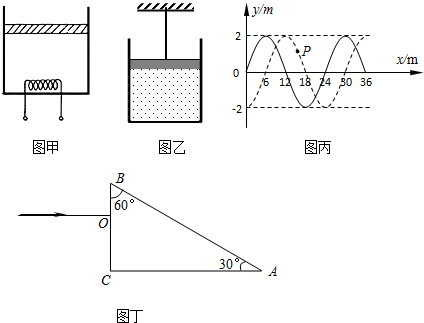
已知在t1时刻简谐横波的波形如图中实线所示;在时刻t2该波的波形如图中虚线所示.t2-t1=0.02s,求:
(1)该波可能的传播速度.
(2)若已知T<t2-t1<2T,且图中P质点在t1时刻的瞬时速度方向向上,求可能的波速.
(3)若0.01s<T<0.02s,且从t1时刻起,图中Q质点比R质点先回到平衡位置,求可能的波速.
(1)该波可能的传播速度.
(2)若已知T<t2-t1<2T,且图中P质点在t1时刻的瞬时速度方向向上,求可能的波速.
(3)若0.01s<T<0.02s,且从t1时刻起,图中Q质点比R质点先回到平衡位置,求可能的波速.

(1)若简谐横波是向右传播,在t2-t1内波形向右匀速传播最短距离为
| 1 |
| 3 |
根据波的周期性得波传播的距离为x=(n+
| 1 |
| 3 |
波速v=
| x |
| t |
(n+
| ||
| t2-t1 |
同理可得若该波是向左传播的,可能的波速v=100(3n+2)m/s (n=0,1,2,…)
(2)P质点速度向上,说明波向左传播,T<t2-t1<2T,说明这段时间内波是向左传播了
| 5 |
| 3 |
则由第(1)问波速表达式v=100(3n+2)m/s (n=0,1,2,…)可知,n取1得到
v=500m/s
(3)“Q比R先回到平衡位置”,说明波是向右传播的.由题0.01s<T<0.02s,即
| t2-t1 |
| 2 |
也就是T<t2-t1<2T,则这段时间内波只可能向右传播了
| 4 |
| 3 |
由第(1)问波速表达式v=100(3n+1)m/s (n=0,1,2,…)可知,n取1
得到v=400m/s.
答:(1)该波可能的传播速度为:若简谐横波是向右传播,波速v=100(3n+1)m/s (n=0,1,2,…);
若波是向左传播的,波速v=100(3n+2)m/s (n=0,1,2,…)
(2)若已知T<t2-t1<2T,且图中P质点在t1时刻的瞬时速度方向向上,可能的波速为500m/s.
(3)若0.01s<T<0.02s,且从t1时刻起,图中Q质点比R质点先回到平衡位置,可能的波速为400m/s.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目

 注入人体,参与人体的代谢过程.
注入人体,参与人体的代谢过程. 在人体内衰变放出正电子,与人体内负电子相遇而湮灭转化为一对光子,被探测器探测到,经计算机处理后产生清晰的图象.根据PET原理,回答下列问题:
在人体内衰变放出正电子,与人体内负电子相遇而湮灭转化为一对光子,被探测器探测到,经计算机处理后产生清晰的图象.根据PET原理,回答下列问题: 的衰变的方程式______8O→
的衰变的方程式______8O→ N+
N+ e
e