题目内容
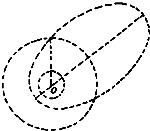 宇宙飞船在距火星表面H高度处作匀速圆周运动,火星半径为R,今设飞船在极短时间内向外侧点喷气,使飞船获得一径向速度,其大小为原速度的α倍,因α量很小,所以飞船新轨道不会与火星表面交会,如图所示,飞船喷气质量可忽略不计.
宇宙飞船在距火星表面H高度处作匀速圆周运动,火星半径为R,今设飞船在极短时间内向外侧点喷气,使飞船获得一径向速度,其大小为原速度的α倍,因α量很小,所以飞船新轨道不会与火星表面交会,如图所示,飞船喷气质量可忽略不计.(1)试求飞船新轨道的近火星点的高度h近,和远火星点高度h远.
(2)设飞船原来的运动速度为v0,试计算新轨道的运行周期T.
分析:(1)根据开普勒定律中的面积定律、机械能守恒定律、牛顿第二定律列式后联立求解;
(2)根据开普勒定律中的周期定律列式求解.
(2)根据开普勒定律中的周期定律列式求解.
解答:解:(1)设火星和飞船的质量分别为M和m,飞船沿椭圆轨道运行时,飞船在最近点或最远点与火星中心的距离为r,飞船速度为v.
因飞船喷气前绕圆轨道的面积速度为
r0v0,等于喷气后飞船绕椭圆轨道在P点的面积速度
r0vpsinθ(P为圆和椭圆的交点),
由开普勒第二定律,后者又应等于飞船在近、远火星的面积速度
rv,
故
r0v0=
r0vpsinθ=
rv
即 r0v0=rv ①
由机械能守恒定律
mv2-G
=
m(
+a2
)-G
②
飞船沿原圆轨道运动时,有 G
=m
③
式中 r0=R+H,r=R+h
上述三个方程消去G、M、v0后可解得关于r的方程为(1-α2)r2-2r0r+
=0
上式有两个解,大者为r远,小者为r近,即
故近、远火星点距火星表面的高度为h近=r近-R=
,h远=r远-R=
,
(2)设椭圆轨道的半长轴为a,则r近+r远=2a
即 a=
飞船喷气前绕圆轨道运行的周期为 T0=
设飞船喷气后,绕椭圆轨道运行的周期为T,由开普勒第三定律得
=(
)3/2
故T=T0(
)3/2=
(
)3/2
T=
(
)3/2
答:(1)试求飞船新轨道的近火星点的高度h近为
,远火星点高度h远为
;
(2)计算新轨道的运行周期T为
(
)3/2.
因飞船喷气前绕圆轨道的面积速度为
| 1 |
| 2 |
| 1 |
| 2 |
由开普勒第二定律,后者又应等于飞船在近、远火星的面积速度
| 1 |
| 2 |
故
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
即 r0v0=rv ①
由机械能守恒定律
| 1 |
| 2 |
| Mm |
| r |
| 1 |
| 2 |
| v | 2 0 |
| v | 2 0 |
| Mm |
| r0 |
飞船沿原圆轨道运动时,有 G
| Mm | ||
|
| ||
| r0 |
式中 r0=R+H,r=R+h
上述三个方程消去G、M、v0后可解得关于r的方程为(1-α2)r2-2r0r+
| r | 2 0 |
上式有两个解,大者为r远,小者为r近,即
|
故近、远火星点距火星表面的高度为h近=r近-R=
| H-αR |
| 1+α |
| H+αR |
| 1-α |
(2)设椭圆轨道的半长轴为a,则r近+r远=2a
即 a=
| r0 |
| 1-α2 |
飞船喷气前绕圆轨道运行的周期为 T0=
| 2πr0 |
| v0 |
设飞船喷气后,绕椭圆轨道运行的周期为T,由开普勒第三定律得
| T |
| T0 |
| a |
| r0 |
故T=T0(
| a |
| r0 |
| 2πr0 |
| v0 |
| 1 |
| 1-α2 |
T=
| 2π(R+H) |
| v0 |
| 1 |
| 1-α2 |
答:(1)试求飞船新轨道的近火星点的高度h近为
| H-αR |
| 1+α |
| H+αR |
| 1-α |
(2)计算新轨道的运行周期T为
| 2π(R+H) |
| v0 |
| 1 |
| 1-α2 |
点评:本题是开普勒定律和机械能守恒定律的综合运用问题,目前对于开普勒三定律,多数省份是不要求定量计算的,较难.

练习册系列答案
相关题目
