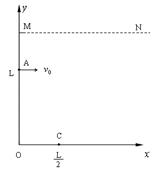
题目内容
如图,在xoy平面第一象限内有平行于y轴的匀强电场和垂直于xoy平面的匀强磁场,匀强电场电场强度为E。一带电量为+q的小球从y轴上离坐标原点距离为L的A点处,以沿x正向的初速度进入第一象限,如果电场和磁场同时存在,小球将做匀速圆周运动,并从x轴上距坐标原点L/2的C点离开磁场。如果只撤去磁场,并且将电场反向,带电小球以相同的初速度从A点进入第一象限,仍然从x轴上距坐标原点L/2的C点离开电场。求:
(1)小球从A点出发时的初速度大小;
(2)磁感应强度B的大小和方向;
(3)如果在第一象限内存在的磁场范围是一个矩形,求这一范围的最小面积。
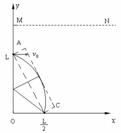
解:(1)由带电小球做匀速圆周运动知,mg=Eq (2分)
所以电场反向后竖直方向受力 Eq+mg=ma a=2g (2分)
小球做类平抛运动有L/2=v0t , L=![]() 2gt2 (2分)
2gt2 (2分)
得 v0=![]()
![]() (2分)
(2分)
(2)带电小球做匀速圆周运动时,洛仑兹力提供向心力
qv0B =mv02/R B=mv0/(qR ) (2分)
由圆周运动轨迹分析得 (L-R)2+(![]() )2=R2 (2分)
)2=R2 (2分)
R=5L/8
代入得B=![]() (2分)
(2分)
(3)由小球运动轨迹的范围知最小矩形磁场的长、宽分别为
a2 = (L)2+(![]() )2 a =
)2 a =![]() L/2 (2分) b = R-R
L/2 (2分) b = R-R![]() =(5-
=(5-![]() )L/8 (2分)
)L/8 (2分)
面积S=5(![]() -1)L2/16 (2分)
-1)L2/16 (2分)

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案 如图,在xOy平面内,第I象限中有匀强电场,场强大小为E,方向沿y轴正方向.在x轴的下方有匀强磁场,磁场方向垂直于纸面向里,电、磁场区域足够大.今有一个质量为m、电荷量为e的电子(不计重力),从y轴上的P点以初速度v0垂直于电场方向进入电场,经电场偏转后,沿着x轴正方向成45°角进入磁场,并能返回到原出发点P. 求:
如图,在xOy平面内,第I象限中有匀强电场,场强大小为E,方向沿y轴正方向.在x轴的下方有匀强磁场,磁场方向垂直于纸面向里,电、磁场区域足够大.今有一个质量为m、电荷量为e的电子(不计重力),从y轴上的P点以初速度v0垂直于电场方向进入电场,经电场偏转后,沿着x轴正方向成45°角进入磁场,并能返回到原出发点P. 求: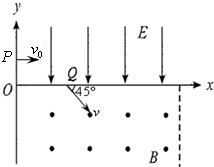 (2013?马鞍山三模)如图,在xoy平面第一象限整个区域分布匀强电场,电场方向平行y轴向下,在第四象限内存在有界匀强磁场,左边界为y轴,右边界为x=
(2013?马鞍山三模)如图,在xoy平面第一象限整个区域分布匀强电场,电场方向平行y轴向下,在第四象限内存在有界匀强磁场,左边界为y轴,右边界为x= 如图,在xOy平面的第一、四象限内存在着方向垂直纸面向外、磁感应强度为B的匀强磁场,第四象限内存在方向沿-y方向、电场强度为E的匀强电场.从y轴上坐标为a的一点向磁场区发射速度大小不等的带正电同种粒子,速度方向范围是与+y方向成(30°-150°),且在xOy平面内.结果所有粒子经过磁场偏转后都垂直打到x轴上,然后进入第四象限的匀强电场区.已知带电粒子电量为+q,质量为m,重力不计.
如图,在xOy平面的第一、四象限内存在着方向垂直纸面向外、磁感应强度为B的匀强磁场,第四象限内存在方向沿-y方向、电场强度为E的匀强电场.从y轴上坐标为a的一点向磁场区发射速度大小不等的带正电同种粒子,速度方向范围是与+y方向成(30°-150°),且在xOy平面内.结果所有粒子经过磁场偏转后都垂直打到x轴上,然后进入第四象限的匀强电场区.已知带电粒子电量为+q,质量为m,重力不计.

