题目内容
(1)一简谐运动的位移与时间的函数关系式为 ,由此可以求出该运动的周期为______s,初相位为______
,由此可以求出该运动的周期为______s,初相位为______(2)如图所示直角三角形透明体,∠A=60°;∠B=30°.一束单色光垂直AC边射入透明体,先在AB面发生全反射,然后一部分光线从CB边上的某点射出,该出射光线与CB边成45°角,另一部分从AB上的某点射出.请使用铅笔(笔迹适当黑些、粗些)画出光路图(画出有关的箭头和辅助线,注明有关角度的大小),求出该透明体的折射率.

【答案】分析:(1)由解析式读出ω=80πrad/s,初相位为 .求出周期.
.求出周期.
(2)单色光垂直AC边射入透明体,方向不变射到AB面上,入射角等于60°,经全反射射到BC面上时,入射角是30°,折射角是45°,作出光路图.由折射定律求解折射率.
解答:解:
(1)简谐运动的位移与时间的函数关系式为 ,式中ω=80πrad/s,初相位为
,式中ω=80πrad/s,初相位为 .则周期T=
.则周期T= =0.025s.
=0.025s.
(2)光路图如图所示.由几何知识得到,i=30°,根据公式 ,
,
代入解得
故答案为:(1)0.025; .
.
(2)该透明体的折射率是1.414.
点评:本题是基础题,考查运用几何知识分析和处理几何光学的能力.
 .求出周期.
.求出周期.(2)单色光垂直AC边射入透明体,方向不变射到AB面上,入射角等于60°,经全反射射到BC面上时,入射角是30°,折射角是45°,作出光路图.由折射定律求解折射率.
解答:解:

(1)简谐运动的位移与时间的函数关系式为
 ,式中ω=80πrad/s,初相位为
,式中ω=80πrad/s,初相位为 .则周期T=
.则周期T= =0.025s.
=0.025s.(2)光路图如图所示.由几何知识得到,i=30°,根据公式
 ,
,代入解得

故答案为:(1)0.025;
 .
.(2)该透明体的折射率是1.414.
点评:本题是基础题,考查运用几何知识分析和处理几何光学的能力.

练习册系列答案
相关题目
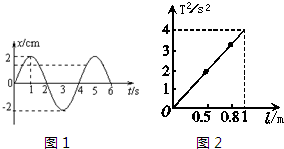 (1)一个质点做简谐运动的图象如图所示,质点振动频率为
(1)一个质点做简谐运动的图象如图所示,质点振动频率为