题目内容
如图所示，等腰直角三棱镜放在真空中，斜边BC=d，一束单色光以60°的入射角从AB侧面中点入射，折射后再从AC侧面折射出，已知三棱镜的折射率n=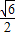
，单色光在真空中的光速为c，求此单色光通过三棱镜的时间．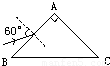
【答案】分析：光在AB面上入射角为60°，根据折射定律求出折射角，根据几何知识求出光在三棱镜中传播的距离，由v=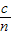
求出光在三棱镜传播的速度，再求此单色光通过三棱镜的时间．
解答：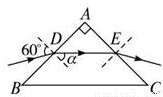
解：单色光在AB面上发生折射，光路图如图．
根据折射定律得，n=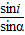
=
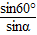，n=
，
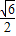代入解得，α=45°，光线射到AC面上时入射角为45°，从AC射出三棱镜．根据几何知识得知，DE∥BC，而且DE=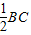
=
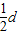
光在三棱镜传播的速度为v=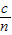
=
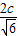
所以此单色光通过三棱镜的时间t=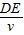
=
．
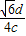答：此单色光通过三棱镜的时间t=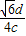
．
点评：本题是简单的几何光学问题，作出光路图是解答的基础，本题是折射定律和光速公式v=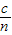
的综合应用．
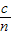求出光在三棱镜传播的速度，再求此单色光通过三棱镜的时间．解答：
解：单色光在AB面上发生折射，光路图如图．根据折射定律得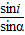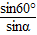，n=
=，n=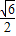，代入解得，α=45°，光线射到AC面上时入射角为45°，从AC射出三棱镜．根据几何知识得知，DE∥BC，而且DE=
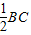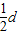
=光在三棱镜传播的速度为v=
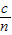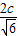
=所以此单色光通过三棱镜的时间t=
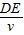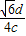=．答：此单色光通过三棱镜的时间t=
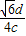．点评：本题是简单的几何光学问题，作出光路图是解答的基础，本题是折射定律和光速公式v=
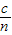的综合应用． 
练习册系列答案
相关题目
如图所示，等腰直角三角形ABC，O为斜边AC边的中点．在A、B、C三个顶点处分别放置三根通电长直导线，导线中的电流大小相等，方向均垂直纸面向里．则三根通电直导线在O点共同产生的磁场的方向为图中（ ）
如图所示是等腰直角三棱柱，其中底面abcd为正方形，边长为L，它们按图示位置放置于竖直向下的匀强磁场中，磁感应强度为B，下面说法中正确的是（ ）如图所示是等腰直角三棱柱，其中底面abcd为正方形，边长为L，它们按图示位置放置于竖直向下的匀强磁场中，磁感应强度为B，下面说法中正确的是( )
| A．通过abcd平面的磁通量大小为L2·B |
B．通过dcfe平面的磁通量大小为 L2·B |
| C．通过abfe平面的磁通量大小为零 |
| D．通过bcf平面的磁通量为零 |
L2·B 
