题目内容
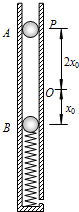 质量均为m的小球B用一根轻质弹簧竖直固定的内壁光滑的直圆筒内,平衡时弹簧的压缩量为x0,如图所示.设弹簧的弹性势能与弹簧的形变量(即伸长量或缩短量)的平方成正比.小球A从小球B的正上方距离为3x0的P处自由落下,落在小球B上立刻与小球B粘连在一起向下运动,它们达到最低点后又向上运动,已知小球A的质量也为m时,它们恰能回到O点(设两个小球直径相等,且远小于x0,略小于直圆管内径),求:
质量均为m的小球B用一根轻质弹簧竖直固定的内壁光滑的直圆筒内,平衡时弹簧的压缩量为x0,如图所示.设弹簧的弹性势能与弹簧的形变量(即伸长量或缩短量)的平方成正比.小球A从小球B的正上方距离为3x0的P处自由落下,落在小球B上立刻与小球B粘连在一起向下运动,它们达到最低点后又向上运动,已知小球A的质量也为m时,它们恰能回到O点(设两个小球直径相等,且远小于x0,略小于直圆管内径),求:(1)两个小球及弹簧组成的系统在上述过程中机械能是否守恒;
(2)弹簧初始时刻的机械能;
(3)小球A与小球B一起向下运动时速度的最大值.
分析:(1)根据系统机械能守恒的条件判断在各个过程中是否守恒即可;
(2)弹簧从原长压缩到x0的过程中,弹簧力与位移成线性关系,求出克服弹簧力的功,最大弹力等于物体的重力,且克服弹簧力的功等于弹簧增加的弹性势能,所以,弹簧被压缩后即初始时刻的弹性势能;
(3)当弹簧的弹力等于A、B两球的总重力时,小球A、B的速度最大,根据力的平衡求出两球下降的距离,再对系统运用机械能守恒定律,求出最大速度.
(2)弹簧从原长压缩到x0的过程中,弹簧力与位移成线性关系,求出克服弹簧力的功,最大弹力等于物体的重力,且克服弹簧力的功等于弹簧增加的弹性势能,所以,弹簧被压缩后即初始时刻的弹性势能;
(3)当弹簧的弹力等于A、B两球的总重力时,小球A、B的速度最大,根据力的平衡求出两球下降的距离,再对系统运用机械能守恒定律,求出最大速度.
解答:解:(1)整个系统在A下落到与B碰撞前,只有重力做功,机械能守恒;AB碰撞的过程中,系统机械能不守恒;AB碰撞后至回到O点过程中,机械能守恒;
(2)弹簧从原长压缩到x0的过程中,弹簧力与位移成线性关系,所以,克服弹簧力的功可以由平均力求出:W=
x0,
最大弹力等于物体的重力,且克服弹簧力的功等于弹簧增加的弹性势能,所以,弹簧被压缩后即初始时刻的弹性势能EP=W=
mgx0
(3)设A与B接触时的速度为v1,由机械能守恒,
mg?3x0=
mv12,
解得:v1=
二物体相碰过程动量守恒m v1=2mv2,粘合后速度 v2=
.
A和B粘合后加速下行,当弹簧弹力等于二物体总重力时速度达到最大,此时弹簧压缩量为2x0,设最大速度为vm.设达到最大速度时弹簧的弹性势能为E′P,由题设条件可知
E′P=4EP=2mgx0
二物体粘合后机械能守恒,取速度最大处为零势能面,则
EP+
×2mv22+2mgx0=E′P+
×2mvm2
解得vm=
答:(1)整个系统在A下落到与B碰撞前,机械能守恒;AB碰撞的过程中,系统机械能不守恒;AB碰撞后至回到O点过程中,机械能守恒;
(2)弹簧初始时刻的机械能为
mgx0;
(3)小球A与小球B一起向下运动时速度的最大值为
.
(2)弹簧从原长压缩到x0的过程中,弹簧力与位移成线性关系,所以,克服弹簧力的功可以由平均力求出:W=
| Fm |
| 2 |
最大弹力等于物体的重力,且克服弹簧力的功等于弹簧增加的弹性势能,所以,弹簧被压缩后即初始时刻的弹性势能EP=W=
| 1 |
| 2 |
(3)设A与B接触时的速度为v1,由机械能守恒,
mg?3x0=
| 1 |
| 2 |
解得:v1=
| 6gx0 |
二物体相碰过程动量守恒m v1=2mv2,粘合后速度 v2=
| 1 |
| 2 |
| 6gx0 |
A和B粘合后加速下行,当弹簧弹力等于二物体总重力时速度达到最大,此时弹簧压缩量为2x0,设最大速度为vm.设达到最大速度时弹簧的弹性势能为E′P,由题设条件可知
E′P=4EP=2mgx0
二物体粘合后机械能守恒,取速度最大处为零势能面,则
EP+
| 1 |
| 2 |
| 1 |
| 2 |
解得vm=
| 2gx0 |
答:(1)整个系统在A下落到与B碰撞前,机械能守恒;AB碰撞的过程中,系统机械能不守恒;AB碰撞后至回到O点过程中,机械能守恒;
(2)弹簧初始时刻的机械能为
| 1 |
| 2 |
(3)小球A与小球B一起向下运动时速度的最大值为
| 2gx0 |
点评:本题综合运用了动能定理、动量守恒定律、机械能守恒定律,综合性较强,关键是选择好研究的过程,运用合适的规律列表达式求解.

练习册系列答案
相关题目
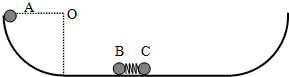 如图所示,光滑固定轨道的两端都是半径为R的四分之一圆弧,在轨道水平面上有两个质量均为m的小球B、C,B、C用一长度锁定不变的轻小弹簧栓接,弹性势能
如图所示,光滑固定轨道的两端都是半径为R的四分之一圆弧,在轨道水平面上有两个质量均为m的小球B、C,B、C用一长度锁定不变的轻小弹簧栓接,弹性势能 如图所示,一根长为l的轻质直杆,可绕光滑转轴O自由转动,在其中点、上端分别固定质量均为m的小球B、A,小球A用水平绳系住,使杆与水平面成53°角.
如图所示,一根长为l的轻质直杆,可绕光滑转轴O自由转动,在其中点、上端分别固定质量均为m的小球B、A,小球A用水平绳系住,使杆与水平面成53°角. .一质量也为m的小球A从左侧的最高点自由滑下,A滑到水平面与B碰后立即粘在一起结合成D就不再分离(碰撞时间极短).当D、C一起刚要滑到右侧最低点时,弹簧锁定解除且立即将C弹出并与弹簧分离.求
.一质量也为m的小球A从左侧的最高点自由滑下,A滑到水平面与B碰后立即粘在一起结合成D就不再分离(碰撞时间极短).当D、C一起刚要滑到右侧最低点时,弹簧锁定解除且立即将C弹出并与弹簧分离.求