题目内容
如图所示一个质量为0.2 kg的小球用细线吊在倾角为θ＝53°的斜面体的顶端，斜面体静止时球紧靠在斜面上，细线与斜面平行，不计摩擦，当斜面以10 m/s2加速度向左运动时，求绳子的拉力及斜面对小球的弹力的大小．(g取10 m/s2)
答案：
解析：
解析：
|
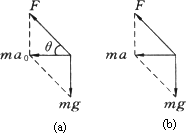
分析：我们可用极限分析法判断临界状态．若加速度较小，则小球对斜面有压力，绳平行斜面，若加速度较大，则球将“飘起”．绳不再与斜面平行．则小球即将飘起时为临界状态．
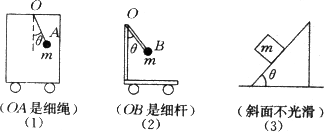
注意：①“极限分析法”是分析临界状态行之有效的方法． ②牛顿运动定律中经常遇到以下情况：如图所示．
③装置均向左做匀加速运动： 若a＝gtanθ：装置(2)杆的作用力沿杆向上． 装置(3)m与斜面间无相对运动趋势． 若a＞gtanθ：装置(1)θ增大． 装置(2)杆的作用力偏向杆的下方． 装置(3)m相对斜面有向上运动的趋势，摩擦力沿斜面向下． 若a＜gtanθ：装置(1)θ减小 装置(2)杆的作用力偏向杆的上方． 装置(3)m相对斜面有向下运动趋势，摩擦力沿斜面向上． 可见：a＝gtanθ是状态变化的临界点． |
练习册系列答案
相关题目
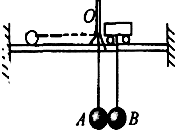如图所示，质量为0.3kg的小车静止在光滑的轨道上，在它下面挂一个质量为0.1kg的小球B，车旁有一支架被固定在轨道上，支架上O点悬挂一质量也为0.1kg的小球A，两球的球心至悬挂点的距离均为0.2m．当两球静止时刚好相切，两球心位于同一水平线，两条悬线竖直且相互平行．若将A球向左拉至图中虚线所示位置后从静止释放，与B球发生碰撞，碰撞中无机械能损失，求碰后B球上升的最大高度．（重力加速度g=10m/s2）
如图所示，质量为0.8kg的物块以5m/s的初速度从斜面顶端下滑，斜面长5m，倾角为37°，物块与斜面间的动摩擦因数为μ=0.2，（已知sin37°=0.6，cos37°=0.8，g=10m/s2）求：