Question

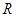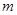（10分）如图所示，空间存在水平向右的匀强电场. 在竖直平面内建立平面直角坐标系，在坐标系的一象限内固定绝缘光滑的半径为的1/4圆周轨道，轨道的两端在坐标轴上。质量为的带正电的小球从轨道的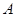端由静止开始滚下，已知重力为电场力的2倍，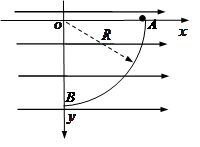

求：（1）小球在轨道最低点时对轨道的压力；
（2）小球脱离点后开始计时，经过多长时间小球运动到点的正下方？并求出此时小球距的竖直高度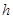是多大？

Answer 1

（1）2mg   (2)   8R

解析试题分析：(1) 小球从释放到运动至轨道最低点的过程中，由动能定理得：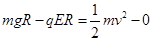
 （2分），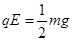
在轨道最低点时，有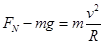： （2分）
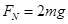联立上述各式得：（1分），（1分）
(2)小球的运动，在竖直方向是自由落体运动，水平方向是往返运动。
由运动的分解可知，当水平速度变为零时，有：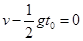
（1分）   得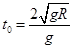：（1分）
设经历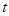运动到B点的正下方，则:  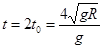（1分）
在竖直方向上，有: 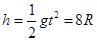（1分）
考点：电场中圆周运动的问题
点评：此题较难。解决此类问题只需要把电场力看成一个普通的恒力分析就行了；分析问题时一定要弄清物体的运动轨迹，是什么运动。