题目内容
如图所示,装置BO′O可绕竖直轴O′O转动,可视为质点的小球A与两细线连接后分别系于B、C两点,装置静止时细线AB水平,细线AC与竖直方向的夹角θ=37º.已知小球的质量m=1kg,细线AC长l=1m, B点距C点的水平和竖直距离相等.(重力加速度g取10m/s2,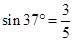 ,
,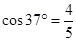 )(结果可以用根号表示)
)(结果可以用根号表示)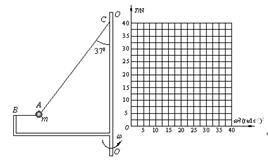
(1)若装置匀速转动的角速度为ω1时,细线AB上的张力为零而细线AC与竖直方向夹角仍为37º,求角速度ω1的大小;
(2)若装置匀速转动的角速度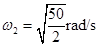 ,求细线AC与竖直方向的夹角的余弦值;
,求细线AC与竖直方向的夹角的余弦值;
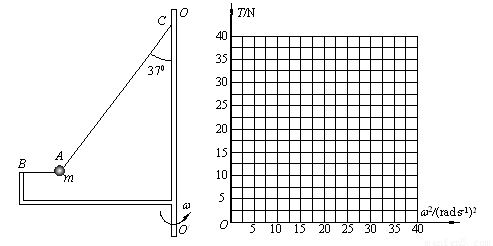
(3)装置可以以不同的角速度匀速转动,试通过计算在坐标图中画出细线AC上张力T随角速度的平方ω2 变化的关系图象。
(1)  (2)
(2) (3)
(3) 
解析试题分析:(1)细线AB上张力恰为零时有: (2分)
(2分)  (2分)
(2分) (2分)
(2分)
有上式得: (1分)
(1分)
解得  (1分)
(1分)
(2)有几何关系可得,当AB上有拉力时,细线AB处于竖直方向。
设细线AB恰好竖直,但张力为零时有: (2分)
(2分)
有几何关系可得: (1分)
(1分)
故有 (1分)
(1分)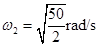 >
> (1分)
(1分)
可得:
此时细线AB恰好竖直,
 (1分)
(1分)
(3) 时,细线AB水平,细线AC上张力的竖直分量等于小球的重力
时,细线AB水平,细线AC上张力的竖直分量等于小球的重力

 时细线AB松弛
时细线AB松弛
细线AC上张力的水平分量等于小球做圆周运动需要的向心力

 时,细线AB在竖直方向绷直,仍然由细线AC上张力的水平分量提供小球做圆周运动需要的向心力
时,细线AB在竖直方向绷直,仍然由细线AC上张力的水平分量提供小球做圆周运动需要的向心力

综上所述 时,
时, 不变
不变 时,
时,
 关系图象如图所示
关系图象如图所示
在 (rad.s-1)2的区间画出T=12.5N不变的直线得2分,在
(rad.s-1)2的区间画出T=12.5N不变的直线得2分,在 (rad.s-1)2的区间画出
(rad.s-1)2的区间画出 的直线且该直线要超出
的直线且该直线要超出 (rad.s-1)2再得2分.
(rad.s-1)2再得2分.
考点:考查了圆锥摆运动
点评:本题的综合性非常强,关键是根据受力分析,判断各种情况下的临界状态,结合牛顿第二定律,圆周运动规律分析解题

 阅读快车系列答案
阅读快车系列答案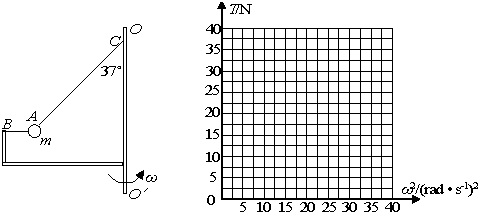
 时,细线AB上的张力为0而细线AC与竖直方向的夹角仍为37°,求角速度
时,细线AB上的张力为0而细线AC与竖直方向的夹角仍为37°,求角速度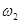 时,细线AB刚好竖直,且张力为0,求此时角速度
时,细线AB刚好竖直,且张力为0,求此时角速度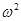 变化的关系图像
变化的关系图像
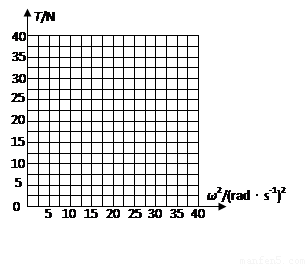
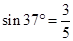 ,
,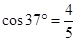 )(结果可以用根号表示)
)(结果可以用根号表示)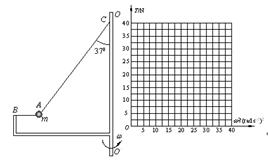
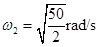 ,求细线AC与竖直方向的夹角的余弦值;
,求细线AC与竖直方向的夹角的余弦值;