Question

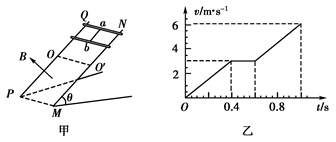
如图甲所示，两根质量均为 0.1kg完全相同的导体棒a、b，用绝缘轻杆相连置于由金属导轨PQ、MN架设的斜面上．已知斜面倾角θ为53°，a、b导体棒的间距是PQ、MN导轨间间距的一半，导轨间分界线OO′以下有方向垂直斜面向上的匀强磁场．当a、b导体棒沿导轨下滑时，其下滑速度v与时间的关系图象如图乙所示．若a、b导体棒接入电路的电阻均为1Ω，其它电阻不计，取g=10m/s²，sin53°≈0.8，cos53°≈0.6，试求：

（1）PQ、MN导轨的间距d；
（2）a、b导体棒与导轨间的动摩擦因数；
（3）匀强磁场的磁感应强度．

Answer 1

分析：（1）根据速度图象分析导体棒的运动情况：导体棒b刚进入磁场时，a、b的连接体做匀速运动，当导体棒a进入磁场后才再次做匀加速运动．则知PQ、MN导轨的间距d等于匀速运动的位移大小x，由图读出匀速运动的时间和速度，x=vt，而d=2x；
（2）两棒未磁场时，一起做匀加速运动，由速度图象的斜率求出加速度，根据牛顿第二定律即可求出的动摩擦因数；
（3）当b导体棒在磁场中做匀速运动时，整体的合力为零，根据平衡条件和安培力公式结合求解磁感应强度．

解答：解：（1）由图乙可知导体棒b刚进入磁场时a、b的连接体做匀速运动，当导体棒a进入磁场后才再次做匀加速运动，因而b棒匀速运动的位移即为a、b棒的间距，
依题意可得：d=2vt=2×3×（0.6-0.4）m=1.2m
（2）设导体棒运动的加速度为a，由图乙得：a=

vt-v0

t

=

3-0

0.4

=7.5(m/s2)
因a、b棒一起运动，故可看作一整体，其受力如图．有牛顿第二定律得：2mgsinθ-μ?2mgcosθ=2ma
故μ=

gsinθ-a

gcosθ

代入解得，μ=0.083
（3）当b导体棒在磁场中做匀速运动时，由平衡条件得：
 2mgsinθ-μ?2mgcosθ-BIL=0
  又I=

BLv

2R

联立解得B=

4mgR(sinθ-μcosθ)/L2v

=

4×0.1×10×1×(0.8-0.083×0.6)/1.22×3

=1/1.2=0.83(T)
答：
（1）PQ、MN导轨的间距为1.2m；
（2）导体棒与导轨间的动摩擦因数大小为0.083；
（3）匀强磁场的磁感应强度大小为0.83T．

点评：本题考查对复杂物理过程的分析能力、从图象读取有用信息的能力．考查运动学知识、牛顿第二定律、闭合电路欧姆定律、法拉第电磁感应定律等知识．考查逻辑推理能力、分析综合运用能力和运用物理知识解决物理问题能力．