题目内容
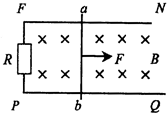 (2004?天津模拟)如图所示,平行金属导轨MN、PQ水平放置,接电阻为R的固定电阻.金属棒ab垂直于导轨放置,且始终与导轨接触良好.导轨和金属棒的电阻不计.匀强磁场方向垂直导轨所在平面.现用垂直于ab棒的水平向右的外力F,拉动ab棒由静止开始向右做匀加速直线运动.则图中哪一个能够正确表示外力F随时间变化的规律?( )
(2004?天津模拟)如图所示,平行金属导轨MN、PQ水平放置,接电阻为R的固定电阻.金属棒ab垂直于导轨放置,且始终与导轨接触良好.导轨和金属棒的电阻不计.匀强磁场方向垂直导轨所在平面.现用垂直于ab棒的水平向右的外力F,拉动ab棒由静止开始向右做匀加速直线运动.则图中哪一个能够正确表示外力F随时间变化的规律?( )分析:ab棒由静止开始向右做匀加速直线运动,则速度为v=at.由E=BLv、I=
和F安=BIL,推导出安培力,再根据牛顿第二定律求得F的表达式,即可进行选择.
| E |
| R |
解答:解:由题意,ab棒由静止开始向右做匀加速直线运动,则其速度为v=at.
由E=BLv、I=
和F安=BIL,得
F安=
=
t
根据牛顿第二定律得:F-F安=ma
联立上两式得:F=
t+ma
式中B、L、a、R均不变,可见F与t是线性关系,C图正确.
故选C
由E=BLv、I=
| E |
| R |
F安=
| B2L2v |
| R |
| B2L2a |
| R |
根据牛顿第二定律得:F-F安=ma
联立上两式得:F=
| B2L2a |
| R |
式中B、L、a、R均不变,可见F与t是线性关系,C图正确.
故选C
点评:安培力是联系电磁感应与力学知识的桥梁,本题关键是推导安培力的表达式,再由牛顿第二定律得到F的表达式.

练习册系列答案
相关题目
 (2004?天津模拟)如图画出了匀强电场的几条电场线,M、N是该电场中的两点.一个带正电荷的离子(不计重力)仅在电场力作用下由M点运动到N点,则( )
(2004?天津模拟)如图画出了匀强电场的几条电场线,M、N是该电场中的两点.一个带正电荷的离子(不计重力)仅在电场力作用下由M点运动到N点,则( )