Question

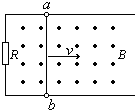如图所示，金属杆ab可在平行金属导轨上滑动，金属杆电阻R₀=0.5Ω，长L=0.3m，导轨一端串接一电阻R=1Ω，匀强磁场磁感强B=2T，当ab以v=5m/s向右匀速运动过程中，求：
（1）ab间感应电动势Ε 和ab间的电压U
（2）所加沿导轨平面的水平外力F的大小
（3）在2s时间内电阻R上产生的热量Q．

Answer 1

分析：（1）导体棒做切割磁感线运动，根据切割公式E=BLV求解感应电动势，然后根据闭合电路欧姆定律求解感应电流和路端电压；
（2）导体棒受拉力和安培力平衡，根据安培力公式F_A=BIL求解安培力，根据平衡条件得到拉力；
（3）根据焦耳定律求解热量即可．

解答：解：（1）根据切割公式E=BLV，有：
E=BLV=2×0.3×5=3V  
感应电流：I=

E

R+r

=

3

1+0.5

=2A
U=IR=2×1=2V           
（2）因是匀速运动．所有受力平衡，有：
F=F_A=BIL=2×2×0.3=1.2N        
（3）2秒电阻R上产生的热量为：
Q=I²Rt=2²×1×2=8J
答：（1）ab间感应电动势Ε为3V，ab间的电压U为2V；
（2）所加沿导轨平面的水平外力F的大小为1.2N；
（3）在2s时间内电阻R上产生的热量Q为8J．

点评：本题关键明确导体棒相当于电源，然后根据切割公式、闭合电路欧姆定律、焦耳定律公式列式求解，基础题．