题目内容
一列沿x轴正方向传播的波，波速为6m/s，振幅为2cm，在某一时刻距波源5cm的A点运动到负最大位移时，距波源8cm的B点恰在平衡位置且向上运动．可知该波的波长λ，频率f分别为（ ）分析：根据A、B两个质点的振动状态，结合波形确定A、B距离与波长的关系式，再求出波长．由波速公式求解频率．
解答：解：由题，波沿x轴正方向传播，在某一时刻距波源5cm的A点运动到负最大位移时，距波源8cm的B点恰在平衡位置且向上运动，根据波形得到，AB间至少是
完整波形，则A、B间距离△x=（n+
）λ，n=0，1，2，…
波长λ=
=
cm=
cm．
当n=0时，λ=4cm，由波速公式v=λf得，频率f=
=
Hz=150Hz．
由于n是整数，λ不可能等于12cm．
故选B
| 3 |
| 4 |
| 3 |
| 4 |
波长λ=
| 4△x |
| 4n+3 |
| 4×(8-5) |
| 4n+3 |
| 12 |
| 4n+3 |
当n=0时，λ=4cm，由波速公式v=λf得，频率f=
| v |
| λ |
| 6 |
| 0.04 |
由于n是整数，λ不可能等于12cm．
故选B
点评：本题考查根据两个质点在同一时刻的状态，研究波长与质点间距离关系的能力，往往要画出波形研究．
练习册系列答案
夺冠金卷全能练考系列答案
相关题目
（2006?重庆）如图为一列沿x轴正方向传播的简谐横波在t=0时的波形．当R点在t=0时的振动状态传到S点时，PR范围内（含P、R）有一些质点正在向y轴负方向运动，这些质点的x坐标取值范围是（ ）
一列沿x轴正方向传播的简谐横波，在t=0时刻波刚好传播到x=6m处的A点，如图所示，已知波的传播速度为48m/s．请回答下列问题：
（2008?汝城县模拟）在坐标原点的波源 S产生一列沿x轴正方向传播的简谐横波，波速 v=400m/s，已知 t=0时，波刚好传播到 x=40m处，如图所示．在x=400m处有一接收器（图中未画出），则下列说法正确的是 （ ）
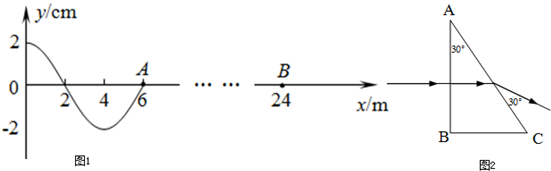
如图所示，一列沿x轴正方向传播的简谐波在某时刻的波形图，其波速为20m/s，则下列说法正确的是（ ）