题目内容
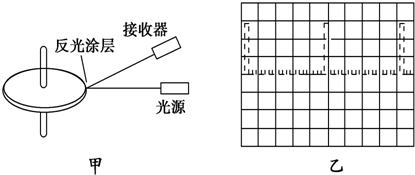
图甲是利用激光测角速度的原理示意图,图中圆盘可绕固定轴转动盘边缘侧面上有一小段涂有很薄的反光材料.当盘转到某一位置时,接收器可以接收到反光涂层所反射的激光束,并将所收到的光信号转变为电信号,在示波器显示屏上显示出来,如图乙所示,
(1)若图乙中示波器显示屏横向每大格(5小格)对应的时间为5.00×10-2s,则圆盘的角速度为
(2)若测得圆盘直径为10.20cm,则可求得圆盘侧面反光涂层的长度为
(1)若图乙中示波器显示屏横向每大格(5小格)对应的时间为5.00×10-2s,则圆盘的角速度为
28.5
28.5
rad/s,(2)若测得圆盘直径为10.20cm,则可求得圆盘侧面反光涂层的长度为
1.46
1.46
cm.
分析:从图象中能够看出圆盘的转动周期即图象中电流的周期,根据角速度与周期的关系式ω=
,即可求出角速度,反光时间即为电流的产生时间;
| 2π |
| T |
解答:解:(1)从图乙显示圆盘转动一周在横轴上显示22格,由题意知道,每格表示1.00×10-2s,所以圆盘转动的周期为0.22秒,
则根据角速度与周期的关系式ω=
,即可求出角速度ω=
rad/s=28.5rad/s;
(2)反光中引起的电流图象在图2中横坐标上每次一小格,说明反光涂层的长度占圆盘周长的22分之一,故圆盘上反光涂层的长度为
=
=1.46cm;
故答案为:28.5,1.46.
则根据角速度与周期的关系式ω=
| 2π |
| T |
| 2×3.14 |
| 0.22 |
(2)反光中引起的电流图象在图2中横坐标上每次一小格,说明反光涂层的长度占圆盘周长的22分之一,故圆盘上反光涂层的长度为
| πd |
| 22 |
| 3.14×10.2 |
| 22 |
故答案为:28.5,1.46.
点评:本题要注意保留3位有效数字,同时要明确圆盘的转动周期与图象中电流的周期相等,还要能灵活运用转速与周期的关系公式!

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目