题目内容
半径为R的均匀球内切去一个半径为的小球后，质量为M，如图1已知两球内切，在两球心O1、O2的连线上距O1为2R处的质量为m的质点P受到的引力多大？
解析:
这是一个残缺的模型，球壳对P处质点的引力不能
直接应用万有引力定律求解，但是如果将切去的部分填补上去，
使其变成一个完整的均匀球体，一个均匀的球体与一个质点间的
引力即可应用万有引力定律直接计算。填补以后的球体对质点P的
引力是填补上去的球体与球壳对质点P的引力的合力，应用万有
引力定律和力的合成即可求解。
将切去的部分填补上去，设完整球体对质点P的引力为F，球壳部分对质点P的引力为F1 ，填补上去的球体对质点P的引力为F2，则根据题意有 F=F1+F2
根据万有引力定律 F=G ，F2=G
又 M1= ×π（）3=代入F 、F2得
F= , F2=
又 F=F1+F2
∴ F1=F﹣F2=﹣=
练习册系列答案
特高级教师点拨系列答案
相关题目
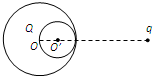如图半径为R的大球O被内切地挖去半径为| R |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
的小球
，余下部分均匀地带有电荷量Q。今在两球球心连线
的延长线上，距大球球心O的距离为r（r＞R）处放置一个点电荷q，求q所受的力。你可以不必进行复杂的计算，而是根据所学的物理知识和物理方法进行分析，从而判断下列解中正确的是（ ）
的小球
，余下部分均匀地带有电荷量Q。今在两球球心连线
的延长线上，距大球球心O的距离为r（r＞R）处放置一个点电荷q，求q所受的力。你可以不必进行复杂的计算，而是根据所学的物理知识和物理方法进行分析，从而判断下列解中正确的是（ ）
B．
D．
的小球
，余下的部分均匀地带有电荷量Q。今在两球球心连线
的延长线上，距大球球心O的距离为r（r＞R）处放置一个点电荷q，求q所受的力。你可以不必进行复杂的计算，而是根据所学的物理知识和物理方法进行分析，从而判断解的合理性。
B．
D．