题目内容
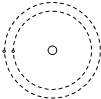（2004?广州二模）火星和地球绕太阳的运动可以看作为同一平面内同方向的匀速圆周运动，已知火星的轨道半径R=1.5×1011m，地球的轨道半径r=1.0×1011m，从如图所示的火星与地球相距最近的时刻开始计时，估算火星再次与地球相距最近需多少地球年？（保留两位有效数字）分析：根据万有引力提供向心力G
=m
r，可得T2=
r3，对于和火星都有同样的关系，所以(
)2=(
)3，这样可以解出火星的周期．两星转过的角度之差△θ=(
-
)t=2 π，可以解得t，即为火星再次与地球相距最近需要的时间．
| mM |
| r2 |
| 4π2 |
| T2 |
| 4π2 |
| GM |
| T1 |
| T2 |
| r1 |
| r2 |
| 2π |
| T1 |
| 2π |
| T2 |
解答：解：设行星质量为m，太阳质量为M，行星与太阳的距离为r，地球的周期为T1，火星的周期为T2，地球的轨道半径为r1，火星的轨道半径为r2．
根据万有引力定律，行星受太阳的万有引力F=G
行星绕太阳做近似匀速圆周运动，
根据牛顿第二定律有F=ma=mω2r
ω═
以上式子联立G
=m
r
故T2=
r3
地球的周期为1年，
(
)2=(
)3
火星的周期为T2=1.8年
设经时间t两星又一次距离最近，
根据θ=ωt
则两星转过的角度之差
△θ=(
-
)t=2 π
得t=2.3年．
答：火星再次与地球相距最近需2.3地球年．
根据万有引力定律，行星受太阳的万有引力F=G
| mM |
| r2 |
行星绕太阳做近似匀速圆周运动，
根据牛顿第二定律有F=ma=mω2r
ω═
| 2π |
| T |
以上式子联立G
| mM |
| r2 |
| 4π2 |
| T2 |
故T2=
| 4π2 |
| GM |
地球的周期为1年，
(
| T1 |
| T2 |
| r1 |
| r2 |
火星的周期为T2=1.8年
设经时间t两星又一次距离最近，
根据θ=ωt
则两星转过的角度之差
△θ=(
| 2π |
| T1 |
| 2π |
| T2 |
得t=2.3年．
答：火星再次与地球相距最近需2.3地球年．
点评：本题也可运用开普勒周期定律
=k求解火星的周期，这种方法更简洁．此题难度不大，属于中档题．
| a3 |
| T2 |
练习册系列答案
相关题目
（2004?广州二模）“二分频”音箱内有两个不同口径的扬声器，它们的固有频率分别处于高音、低音频段，分别称为高音扬声器和低音扬声器，音箱要将扩音机送来的含有不同频率的混合音频电流按高、低频段分离出来，送往相应的扬声器，以便使电流所携带的音频信息按原比例还原成高、低频的机械振动图为音箱的电路图，高、低频混合电流由a、b输入，L1和L2是线圈，C1和C2是电容器（ ）
（2004?广州二模）如图所示，绝缘光滑的半圆轨道位于竖直平面内，并处于竖直向下的匀强电场中，在轨道的上缘有一个质量为m，带电荷量为+q的小球，由静止开始沿轨道运动．下列说法正确的是（ ）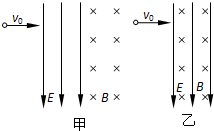
（2004?广州二模）一重力不计的带电粒子一初速度v0先后穿过宽度相同且紧邻在一起的有明显边界的匀强电场E和匀强磁场B，如图甲所示，电场和磁场对粒子总共做功W1；若把电场和磁场正交叠加，如图乙所示，粒子仍以v0的初速度穿过叠加场区对粒子总共做功W2，比较W1、W2的绝对值大小（ ）