题目内容
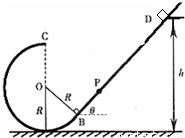
如图所示,倾角为θ=45°的粗糙平直导轨与半径为R的光滑圆环轨道相切,切点为B,整个轨道处在竖直平面内.一质量为m的小滑块从导轨上离地面高为h=3R的D处无初速下滑进入圆环轨道.接着小滑块从圆环最高点C水平飞出,恰好击中导轨上与圆心O等高的P点,不计空气阻力.求:(1)滑块运动到圆环最低点时对圆环轨道压力的大小
(2)滑块与斜轨之间的动摩擦因数.
【答案】分析:对滑块进行运动过程分析,要求滑块运动到圆环最低点时对圆环轨道压力的大小,我们要知道滑块运动到圆环最低点时的速度大小,小滑块从圆环最高点C水平飞出,恰好击中导轨上与圆心O等高的P点,运用平抛运动规律结合几何关系求出最低点时速度.在对最低点运用牛顿第二定律求解.
从D到最低点过程中,再次运用动能定理求解μ.
解答: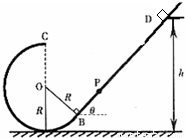 解:(1)小滑块从C点飞出来做平抛运动,水平速度v.
解:(1)小滑块从C点飞出来做平抛运动,水平速度v.
R= gt2,
gt2,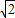 R=vt,
R=vt,
解得:v=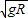
小滑块在最低点时速度为V,由动能定理研究最低点到最高点得:
-mg2R= mv2-
mv2- mv2
mv2
解得:v=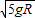
对最低点由牛顿第二定律得:FN-mg=m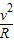
解得:FN=6mg
由牛顿第三定律得:滑块运动到圆环最低点时对圆环轨道压力的大小为6mg.
(2)根据几何关系得:DB之间长度L=(2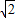 +1)R
+1)R
从D到最低点过程中,运用动能定理得:
mgh-μmgcosθL= mv2
mv2
代入数据得:μ=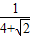 =0.18
=0.18
答:(1)滑块运动到圆环最低点时对圆环轨道压力的大小是6mg,
(2)滑块与斜轨之间的动摩擦因数是0.18.
点评:该题的突破口是小滑块从圆环最高点C水平飞出,恰好击中导轨上与圆心O等高的P点,运用平抛规律和几何关系求出初速度.下面就是一步一步运用动能定理和牛顿第二定律解决问题.
我们在读题时要抓住题目的一些关键语言,这可能就是突破口.
从D到最低点过程中,再次运用动能定理求解μ.
解答:
 解:(1)小滑块从C点飞出来做平抛运动,水平速度v.
解:(1)小滑块从C点飞出来做平抛运动,水平速度v.R=
 gt2,
gt2,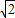 R=vt,
R=vt,解得:v=
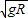
小滑块在最低点时速度为V,由动能定理研究最低点到最高点得:
-mg2R=
 mv2-
mv2- mv2
mv2 解得:v=
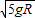
对最低点由牛顿第二定律得:FN-mg=m
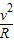
解得:FN=6mg
由牛顿第三定律得:滑块运动到圆环最低点时对圆环轨道压力的大小为6mg.
(2)根据几何关系得:DB之间长度L=(2
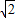 +1)R
+1)R 从D到最低点过程中,运用动能定理得:
mgh-μmgcosθL=
 mv2
mv2代入数据得:μ=
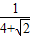 =0.18
=0.18 答:(1)滑块运动到圆环最低点时对圆环轨道压力的大小是6mg,
(2)滑块与斜轨之间的动摩擦因数是0.18.
点评:该题的突破口是小滑块从圆环最高点C水平飞出,恰好击中导轨上与圆心O等高的P点,运用平抛规律和几何关系求出初速度.下面就是一步一步运用动能定理和牛顿第二定律解决问题.
我们在读题时要抓住题目的一些关键语言,这可能就是突破口.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目
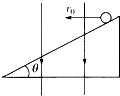 如图所示,倾角为θ的斜面处于竖直向下的匀强电场中,在斜面上某点以初速度为v0水平抛出一个质量为m的带正电小球,小球在电场中受到的电场力与小球所受的重力相等,地球表面重力加速度为g,设斜面足够长.问:
如图所示,倾角为θ的斜面处于竖直向下的匀强电场中,在斜面上某点以初速度为v0水平抛出一个质量为m的带正电小球,小球在电场中受到的电场力与小球所受的重力相等,地球表面重力加速度为g,设斜面足够长.问: 如图所示,倾角为37°、足够长的斜面体固定在水平地面上,小木块在沿斜面向上的恒定外力F作用下,从斜面上的A点由静止开始向上作匀加速运动,前进了4.0m抵达B点时,速度为8m/s.已知木块与斜面间的动摩擦因数μ=0.5,木块质量m=1kg.g取10m/s2,sin37°=0.6,cos37°=0.8.
如图所示,倾角为37°、足够长的斜面体固定在水平地面上,小木块在沿斜面向上的恒定外力F作用下,从斜面上的A点由静止开始向上作匀加速运动,前进了4.0m抵达B点时,速度为8m/s.已知木块与斜面间的动摩擦因数μ=0.5,木块质量m=1kg.g取10m/s2,sin37°=0.6,cos37°=0.8. 如图所示,倾角为θ的斜面上有一质量为m的物体,在水平推力F的作用下移动了距离s,如果物体与斜面间的动摩擦因数为μ,则推力所做的功为( )
如图所示,倾角为θ的斜面上有一质量为m的物体,在水平推力F的作用下移动了距离s,如果物体与斜面间的动摩擦因数为μ,则推力所做的功为( ) (2008?武昌区模拟)如图所示,倾角为θ=30°的光滑绝缘斜面处于电场中,斜面AB长为L,一带电量为+q、质量为m的小球,以初速度υ0由斜面底端的A点开始沿斜面上滑,到达斜面顶端的速度仍为υ0,则( )
(2008?武昌区模拟)如图所示,倾角为θ=30°的光滑绝缘斜面处于电场中,斜面AB长为L,一带电量为+q、质量为m的小球,以初速度υ0由斜面底端的A点开始沿斜面上滑,到达斜面顶端的速度仍为υ0,则( )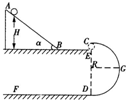 如图所示,倾角为α的光滑斜面与半径为R=0.4m的半圆形光滑轨道在同一竖直平面内,其中斜面与水平面BE光滑连接,水平面BE长为L=0.4m,直径CD沿竖直方向,C、E可看作重合.现有一可视为质点的小球从斜面上距B点竖直距离为H的地方由静止释放,小球在水平面上所受阻力为其重力的
如图所示,倾角为α的光滑斜面与半径为R=0.4m的半圆形光滑轨道在同一竖直平面内,其中斜面与水平面BE光滑连接,水平面BE长为L=0.4m,直径CD沿竖直方向,C、E可看作重合.现有一可视为质点的小球从斜面上距B点竖直距离为H的地方由静止释放,小球在水平面上所受阻力为其重力的