��Ŀ����
��ͼ��ʾ��MN��PQΪˮƽ���õ��㹻����ƽ�й⻬���죬������LΪ0.5m�������������һ��2���ĵ���R����һ������mΪ0.4kg�Ľ�����c d��ֱ�ط��õ����ϣ����뵼��Ӵ����ã��������ĵ���r��СΪ0.5��������ĵ��費�ƣ�����װ�÷��ڴŸ�ǿ��BΪ1T����ǿ�ų��У��ų�����ֱ�ڵ���ƽ�����£��ֶԽ�����ʩ��һˮƽ���ҵ�����F��ʹ���Ӿ�ֹ��ʼ�����˶����������ٶȴﵽ1m/sʱ�������Ĺ���Ϊ0.4w���˿�t=0��ʼ��ʱ�����������Ĺ��ʺ㶨����һ��ʱ��������ﵽ�ȶ��ٶȣ��ڸö�ʱ���ڵ���ͨ������R���Ĺ�Ϊ1.2J��������1�����������ȶ��ٶȣ�
��2���������ӿ�ʼ��ʱֱ���ﵽ�ȶ��ٶ������ʱ�䣻
��3�����������ﵽ�ȶ��ٶȺ�ȥ����F�����������ܻ��ж�Զ��

���𰸡���������1���������Ĺ��ʱ��ֺ㶨�������������ٶȼ�С�ı�����˶�������������˶����ﵽ�ȶ����������Ͱ�����ƽ������ȶ�ʱ�ٶȣ�
��2����������һ���������Ͱ������������������Ĺ���W=Pt�г����ɵ���R�ĵ繦����ܵ繦���ɶ��ܶ������ʱ�䣮
��3����ȥ��������������˶�������ţ�ٵڶ����ɣ��û��ַ�������룮
��� �⣺��1����E=BLv��
�⣺��1����E=BLv�� ��F��=B?I?L���õ�
��F��=B?I?L���õ�
F��=
���������ﵽ�ȶ��ٶ�ʱ
�����Ϲ�ϵʽ�ã�
�������ݵ�v=2m/s
��2��WR=1.2J������
�ɶ��ܶ����ã�
Pt-W��= mv2-
mv2- mv2
mv2
�������ݵ� t=5.25s
��3����ȥ���������ţ�ٵڶ����ɵã�-F��=ma
��
�� ��t=��m
��t=��m
- ��v��t=��m��v
��v��t=��m��v

�����ã�x=8m
�𣺣�1�����������ȶ��ٶ�Ϊ2m/s��
��2���������ӿ�ʼ��ʱֱ���ﵽ�ȶ��ٶ������ʱ��5.25s��
��3�����������ﵽ�ȶ��ٶȺ�ȥ����F�����������ܻ���8m��
�����������ǵ�Ÿ�Ӧ����ѧ֪ʶ���ۺϣ��ѵ��ǵڣ�3����λ�ƣ����ڷ��ȱ����˶�����������ţ�ٵڶ����ɣ��û��ַ����λ�ƣ�
��2����������һ���������Ͱ������������������Ĺ���W=Pt�г����ɵ���R�ĵ繦����ܵ繦���ɶ��ܶ������ʱ�䣮
��3����ȥ��������������˶�������ţ�ٵڶ����ɣ��û��ַ�������룮
���
 �⣺��1����E=BLv��
�⣺��1����E=BLv�� ��F��=B?I?L���õ�
��F��=B?I?L���õ�F��=

���������ﵽ�ȶ��ٶ�ʱ

�����Ϲ�ϵʽ�ã�

�������ݵ�v=2m/s
��2��WR=1.2J������

�ɶ��ܶ����ã�
Pt-W��=
 mv2-
mv2- mv2
mv2�������ݵ� t=5.25s
��3����ȥ���������ţ�ٵڶ����ɵã�-F��=ma
��

��
 ��t=��m
��t=��m
-
 ��v��t=��m��v
��v��t=��m��v
�����ã�x=8m
�𣺣�1�����������ȶ��ٶ�Ϊ2m/s��
��2���������ӿ�ʼ��ʱֱ���ﵽ�ȶ��ٶ������ʱ��5.25s��
��3�����������ﵽ�ȶ��ٶȺ�ȥ����F�����������ܻ���8m��
�����������ǵ�Ÿ�Ӧ����ѧ֪ʶ���ۺϣ��ѵ��ǵڣ�3����λ�ƣ����ڷ��ȱ����˶�����������ţ�ٵڶ����ɣ��û��ַ����λ�ƣ�

��ϰ��ϵ�д�
�����Ŀ
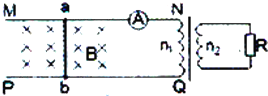 ��ͼ��ʾ��MN��PQ��������ˮƽ���ڡ�ƽ�з��õĹ⻬�������죬������Ҷ˽������ѹ����ԭ��Ȧ����ѹ���ĸ���Ȧ����ֵΪR=0.5���ĵ�����ɱպϻ�·����ѹ����ԭ����Ȧ����֮��n1��n2=2���������ΪL=0.5m������Ϊm=1kg�ĵ����ab��ֱMN��PQ���ڵ����ϣ���ˮƽ���������£���t=0ʱ�̿�ʼ�����˶������ٶ���ʱ��仯�Ĺ�����v=2sin
��ͼ��ʾ��MN��PQ��������ˮƽ���ڡ�ƽ�з��õĹ⻬�������죬������Ҷ˽������ѹ����ԭ��Ȧ����ѹ���ĸ���Ȧ����ֵΪR=0.5���ĵ�����ɱպϻ�·����ѹ����ԭ����Ȧ����֮��n1��n2=2���������ΪL=0.5m������Ϊm=1kg�ĵ����ab��ֱMN��PQ���ڵ����ϣ���ˮƽ���������£���t=0ʱ�̿�ʼ�����˶������ٶ���ʱ��仯�Ĺ�����v=2sin| �� |
| 2 |
A����t=1sʱ�̵�������ʾ��Ϊ
| ||||
| B����������˵�����ѹΪ1V | ||||
| C����λʱ���ڵ���R�ϲ����Ľ�����Ϊ0.25J | ||||
| D����t=0��t=3s��ʱ����ˮƽ���������Ĺ�Ϊ0.75J |
 ��2012?����ģ�⣩��ͼ��ʾ��MN��PQΪ�㹻����ƽ�е��죬���L=O.5m������ƽ����ˮƽ�� ��ļн�6=37�㣬NQ�AMN��NQ��������һ��R=3���ĵ��裮��һ��ǿ�ų���ֱ�� ����ƽ�棬�Ÿ�Ӧǿ��ΪB=1T����һ������Ϊm=0.05kg�Ľ����������ڵ����ϣ��������ĵ���r=2�������ಿ�ֵ��費�ƣ��ִ�ab�ɾ�ֹ�ͷŽ�������ab����NQ���������ص��������˶�������ʼ ����NQƽ�У���֪�������뵼���Ķ�Ħ��������=0.5��������������cd��ʱ�ٶȴ�С��ʼ���ֲ��䣬cd��ab�ľ� ��ΪS=2m����gȡ=10m/s2��
��2012?����ģ�⣩��ͼ��ʾ��MN��PQΪ�㹻����ƽ�е��죬���L=O.5m������ƽ����ˮƽ�� ��ļн�6=37�㣬NQ�AMN��NQ��������һ��R=3���ĵ��裮��һ��ǿ�ų���ֱ�� ����ƽ�棬�Ÿ�Ӧǿ��ΪB=1T����һ������Ϊm=0.05kg�Ľ����������ڵ����ϣ��������ĵ���r=2�������ಿ�ֵ��費�ƣ��ִ�ab�ɾ�ֹ�ͷŽ�������ab����NQ���������ص��������˶�������ʼ ����NQƽ�У���֪�������뵼���Ķ�Ħ��������=0.5��������������cd��ʱ�ٶȴ�С��ʼ���ֲ��䣬cd��ab�ľ� ��ΪS=2m����gȡ=10m/s2�� ��ͼ��ʾ��MN��PQΪ���L=0.5m���㹻����ƽ�е��죬NQ��MN������ ƽ����ˮƽ���ļнǦ�=37�㣬NQ������һ��R=4���ĵ��裮һ��ǿ�ų���ֱ�ڵ���ƽ�棬�Ÿ�Ӧǿ��B=1T����һ������m=0.05kg������r=1���Ľ�����ab������NQ�����ڵ����ϣ����뵼��Ӵ����ã�����ĵ��費�ƣ��־�ֹ�ͷŽ��������������ص��������˶�������ʼ����NQƽ�У���֪�������뵼���Ķ�Ħ��������=0.5����������������cd��ʱ�Ѿ��ﵽ�ȶ��ٶȣ�cd��NQ�ľ���s=0.2m��gȡl0m/s2��sin37��=0.6��cos37��=0.8�� �ʣ�
��ͼ��ʾ��MN��PQΪ���L=0.5m���㹻����ƽ�е��죬NQ��MN������ ƽ����ˮƽ���ļнǦ�=37�㣬NQ������һ��R=4���ĵ��裮һ��ǿ�ų���ֱ�ڵ���ƽ�棬�Ÿ�Ӧǿ��B=1T����һ������m=0.05kg������r=1���Ľ�����ab������NQ�����ڵ����ϣ����뵼��Ӵ����ã�����ĵ��費�ƣ��־�ֹ�ͷŽ��������������ص��������˶�������ʼ����NQƽ�У���֪�������뵼���Ķ�Ħ��������=0.5����������������cd��ʱ�Ѿ��ﵽ�ȶ��ٶȣ�cd��NQ�ľ���s=0.2m��gȡl0m/s2��sin37��=0.6��cos37��=0.8�� �ʣ� ��ͼ��ʾ��MN��PQʽ�̶���ˮƽ���ڼ��L=0.02m��ƽ�н������������ĵ�����Բ��ƣ�������ab��ֱ�����ڹ���ϣ����������������ֵΪR0=1.50���ĵ��裬ab�˵ĵ���R=0.50����ab�������Ӵ����ò�����Ħ��������װ�÷����ڴŸ�Ӧǿ��ΪB=0.50T����ǿ�ų��У��ų�����ֱ���ƽ�����£���ab��ʩ��һˮƽ���ҵ�������ʹ֮��v=5.0m/s���ٶ��ڽ�����������������˶�����
��ͼ��ʾ��MN��PQʽ�̶���ˮƽ���ڼ��L=0.02m��ƽ�н������������ĵ�����Բ��ƣ�������ab��ֱ�����ڹ���ϣ����������������ֵΪR0=1.50���ĵ��裬ab�˵ĵ���R=0.50����ab�������Ӵ����ò�����Ħ��������װ�÷����ڴŸ�Ӧǿ��ΪB=0.50T����ǿ�ų��У��ų�����ֱ���ƽ�����£���ab��ʩ��һˮƽ���ҵ�������ʹ֮��v=5.0m/s���ٶ��ڽ�����������������˶�����