题目内容
 如图所示,一根轻弹簧竖直立在水平面上,下端固定.在弹簧正上方有一个物块从高处自由下落到弹簧上端,将弹簧压缩.当弹簧被压缩了x0时,物块的速度减小到零.从物块和弹簧接触开始到物块速度减小到零过程中,物块加速度大小a随下降位移大小x变化的图象与动能Ek随下降位移大小x变化的图象,正确的是下图中的( )
如图所示,一根轻弹簧竖直立在水平面上,下端固定.在弹簧正上方有一个物块从高处自由下落到弹簧上端,将弹簧压缩.当弹簧被压缩了x0时,物块的速度减小到零.从物块和弹簧接触开始到物块速度减小到零过程中,物块加速度大小a随下降位移大小x变化的图象与动能Ek随下降位移大小x变化的图象,正确的是下图中的( )分析:从物块和弹簧接触开始,弹簧被压缩,弹力与压缩的长度成正比.开始阶段,重力大于弹力,后来重力小于弹力,根据牛顿第二定律分析加速度与位移大小x的关系.若物块从静止开始压缩弹簧,物块做简谐运动,根据简谐运动的对称性,可知物块运动到最低点时加速度大小等于g.当物块以一定的速度压缩弹簧时,物块运动到最低点位置降低,弹簧压缩量增大,根据牛顿第二定律分析加速度与重力加速度的关系,再选择图象.根据物块和弹簧组成的系统机械能守恒研究动能与x的关系,由数学知识选择图象.
解答:解:
A、B从物块和弹簧接触开始分析物块的运动过程:
开始阶段,物块的重力大于弹力,加速度方向向下,根据牛顿第二定律得,mg-kx=ma,得到a=g-
x,a与x是线性关系,而且x增大,a减小;
当重力与弹力平衡时,加速度a=0,物块的速度向下;
当物块的重力小于弹力时,加速度方向向上,根据牛顿第二定律得,kx-mg=ma,得到a=-
x-g,a与x是线性关系,而且x增大,a增大.
若物块从静止开始压缩弹簧,物块做简谐运动,根据简谐运动的对称性,可知物块运动到最低点时加速度大小等于g,方向向上.当物块以一定的速度压缩弹簧时,物块运动到最低点位置降低,弹簧压缩量增大,加速度大于g.故A错误,B正确.
C、D设物块刚接触弹簧时动能为Ek0,以此位置为参考点,根据机械能守恒定律得
Ek0=Ek-mgx+
kx2
则有Ek=Ek0+mgx-
kx2,为开口向下的抛物线.故C正确,D错误.
故选BC
A、B从物块和弹簧接触开始分析物块的运动过程:
开始阶段,物块的重力大于弹力,加速度方向向下,根据牛顿第二定律得,mg-kx=ma,得到a=g-
| k |
| m |
当重力与弹力平衡时,加速度a=0,物块的速度向下;
当物块的重力小于弹力时,加速度方向向上,根据牛顿第二定律得,kx-mg=ma,得到a=-
| k |
| m |
若物块从静止开始压缩弹簧,物块做简谐运动,根据简谐运动的对称性,可知物块运动到最低点时加速度大小等于g,方向向上.当物块以一定的速度压缩弹簧时,物块运动到最低点位置降低,弹簧压缩量增大,加速度大于g.故A错误,B正确.
C、D设物块刚接触弹簧时动能为Ek0,以此位置为参考点,根据机械能守恒定律得
Ek0=Ek-mgx+
| 1 |
| 2 |
则有Ek=Ek0+mgx-
| 1 |
| 2 |
故选BC
点评:本题分析物块的受力情况和运动情况是基础,运用牛顿第二定律列出加速度a与位移x的关系是关键.

练习册系列答案
相关题目
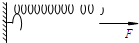 如图所示,一根轻弹簧的一端固定,另一端受到水平拉力F的作用,弹簧的伸长量为x,则此弹簧的劲度系数为( )
如图所示,一根轻弹簧的一端固定,另一端受到水平拉力F的作用,弹簧的伸长量为x,则此弹簧的劲度系数为( )| A、Fx | ||
| B、2Fx | ||
C、
| ||
D、
|
 如图所示,一根轻弹簧竖直放在水平地面上,一个物块从高处自由下落到弹簧上端O,将弹簧压缩,弹簧被压缩x0时物块的速度变为零.从物块与弹簧接触开始,物块的速度v的大小随下降的位移x变化情况与下列四个图象中的哪一个比较一致?( )
如图所示,一根轻弹簧竖直放在水平地面上,一个物块从高处自由下落到弹簧上端O,将弹簧压缩,弹簧被压缩x0时物块的速度变为零.从物块与弹簧接触开始,物块的速度v的大小随下降的位移x变化情况与下列四个图象中的哪一个比较一致?( ) 如图所示,一根轻弹簧在不挂重物时,指针正对刻度5,当挂上80N的重物时,指针正对刻度45,若指针正对刻度35,则所挂重物的重力为(设弹簧的形变始终未超过弹性限度)( )
如图所示,一根轻弹簧在不挂重物时,指针正对刻度5,当挂上80N的重物时,指针正对刻度45,若指针正对刻度35,则所挂重物的重力为(设弹簧的形变始终未超过弹性限度)( ) 如图所示,一根轻弹簧竖立在地面上,其下端和地面固定连接,另外一个小球P从弹簧的正上方、距离弹簧一定高度自由下落,不计空气阻力和碰撞热能损失,则( )
如图所示,一根轻弹簧竖立在地面上,其下端和地面固定连接,另外一个小球P从弹簧的正上方、距离弹簧一定高度自由下落,不计空气阻力和碰撞热能损失,则( ) 如图所示,一根轻弹簧竖直放置,小球从弹簧的正上方某处自由落下,从小球接触弹簧开始到弹簧被压缩到最短的过程中,关于小球的运动,下列说法正确的是( )
如图所示,一根轻弹簧竖直放置,小球从弹簧的正上方某处自由落下,从小球接触弹簧开始到弹簧被压缩到最短的过程中,关于小球的运动,下列说法正确的是( )