题目内容
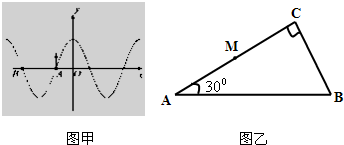
(1)一列简谐横波沿直线ab向右传播,a、b两点之间沿波的传播方向的距离为2m,a、b两点的振动情况如图(1)所示,下列说法中正确的是______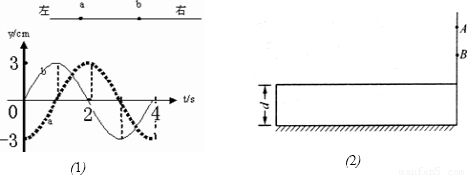
A.波速可能大于
 m/s
m/sB.波速可能等于
 m/s
m/sC.波速可能等于
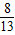 m/s
m/sD.波速可能等于8m/s
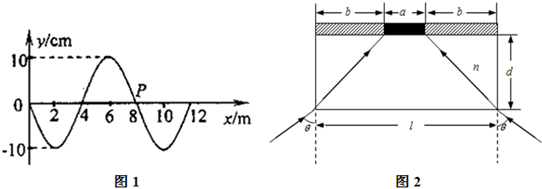
(2)如图(2)所示,两面平行的玻璃砖下表面涂有反射物质,一束与上表面成30°入射的光线,在右端垂直标尺上形成了A、B两个光斑,A、B间距为4cm,已知玻璃砖的折射率为
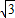 ,画出形成两光斑的光路图,并求此玻璃砖的厚度d.
,画出形成两光斑的光路图,并求此玻璃砖的厚度d.
【答案】分析:(1)根据t=0时刻a、b两质点的振动状态,结合波形,分析a、b间距离与波长的关系,求出波长的通项,再求解波速的通项,求出波速的特殊值.
(2)作出光路图,由折射定律求出折射角,由几何知识求解此玻璃砖的厚度d.
解答: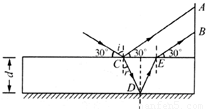 解:(1)由振动图象可知,在t=0时刻,a位于波谷,b经过平衡位置向上,结合波形可知,a、b两点间的距离△x=(n+
解:(1)由振动图象可知,在t=0时刻,a位于波谷,b经过平衡位置向上,结合波形可知,a、b两点间的距离△x=(n+ )λ,(n=0,1,2…)
)λ,(n=0,1,2…)
得 λ= ,则波速为v=
,则波速为v=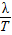 =
=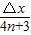 =
=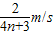
可见,v的最大值为 .
.
当n=1时,v= .
.
故选B
(2)作出光路图,光束入射角i=90°-30°=60°
由n= 得:r=30°
得:r=30°
由几何关系有:CEsin30°=ABsin60°
且CE=2dtsnr
代入数据解得:d=6cm
故答案为:
(1)B
(2)此玻璃砖的厚度d=6cm.
点评:本题中波动图象问题,考虑到波的空间周期性,存在多解.对于几何光学问题,作出光路图是基础,同时要善于运用几何知识求解玻璃砖的厚度.
(2)作出光路图,由折射定律求出折射角,由几何知识求解此玻璃砖的厚度d.
解答:
 解:(1)由振动图象可知,在t=0时刻,a位于波谷,b经过平衡位置向上,结合波形可知,a、b两点间的距离△x=(n+
解:(1)由振动图象可知,在t=0时刻,a位于波谷,b经过平衡位置向上,结合波形可知,a、b两点间的距离△x=(n+ )λ,(n=0,1,2…)
)λ,(n=0,1,2…)得 λ=
 ,则波速为v=
,则波速为v=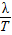 =
=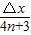 =
=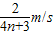
可见,v的最大值为
 .
.当n=1时,v=
 .
.故选B
(2)作出光路图,光束入射角i=90°-30°=60°
由n=
 得:r=30°
得:r=30°由几何关系有:CEsin30°=ABsin60°
且CE=2dtsnr
代入数据解得:d=6cm
故答案为:
(1)B
(2)此玻璃砖的厚度d=6cm.
点评:本题中波动图象问题,考虑到波的空间周期性,存在多解.对于几何光学问题,作出光路图是基础,同时要善于运用几何知识求解玻璃砖的厚度.

练习册系列答案
相关题目

 物理 选修3-4
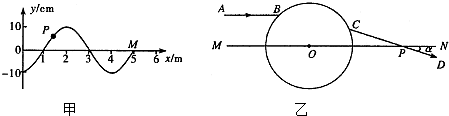
物理 选修3-4 (2009?枣庄一模)(1)一列简谐横波沿x轴传播,图甲是忙3s时的波形图,图乙是波上x=2cm处质点的振动图线.则该波的速度为
(2009?枣庄一模)(1)一列简谐横波沿x轴传播,图甲是忙3s时的波形图,图乙是波上x=2cm处质点的振动图线.则该波的速度为