题目内容
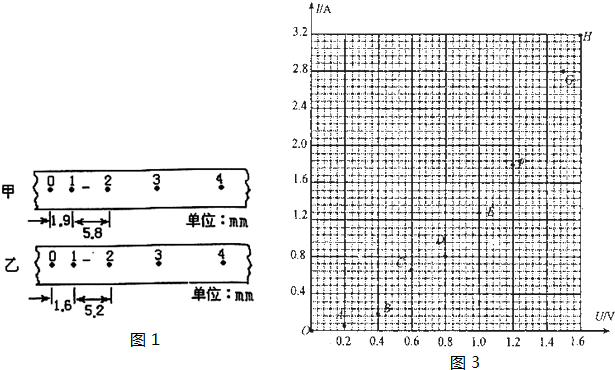
 在“验证机械能守恒定律”的实验中,打点计时器接在电压为E,频率为f的交流电源上,在实验中打下一条理想纸带,如图所示,选取纸带上打出的连续5个点A、B、C、D、E,测出A点距起始点的距离为S0,点AC间的距离为S1,点CE间的距离为S2,已各重锤的质量为m,当地的重力加速度为g,则从起始点O到打下C点的过程中,重锤重力势能的减少量为△EP=
在“验证机械能守恒定律”的实验中,打点计时器接在电压为E,频率为f的交流电源上,在实验中打下一条理想纸带,如图所示,选取纸带上打出的连续5个点A、B、C、D、E,测出A点距起始点的距离为S0,点AC间的距离为S1,点CE间的距离为S2,已各重锤的质量为m,当地的重力加速度为g,则从起始点O到打下C点的过程中,重锤重力势能的减少量为△EP=mg(S0+S1)
mg(S0+S1)
,重锤动能的增加量为△EK=| m(s1+s2)2f2 |
| 32 |
| m(s1+s2)2f2 |
| 32 |
分析:纸带法实验中,若纸带匀变速直线运动,测得纸带上的点间距,利用匀变速直线运动的推论,可计算出打出某点时纸带运动的瞬时速度,从而求出动能.根据功能关系得重力势能减小量等于重力做功的数值.
解答:解:重力势能的减小量等于重力所做功的大小,因此有:W=mgx=mg(S0+S1);
根据匀变速直线运动中时间中点的瞬时速度大小等于该过程中的平均速度大小,因此有:
vC=
=
动能的增量为:△Ek=
m
=
故答案为:mg(S0+S1),
.
根据匀变速直线运动中时间中点的瞬时速度大小等于该过程中的平均速度大小,因此有:
vC=
| S1+S2 |
| 4T |
| f(S1+S2) |
| 4 |
动能的增量为:△Ek=
| 1 |
| 2 |
| v | 2 C |
| m(S1+S2)2f2 |
| 32 |
故答案为:mg(S0+S1),
| m(s1+s2)2f2 |
| 32 |
点评:纸带问题的处理是力学实验中常见的问题,在有纸带处理实验中,若纸带做匀变速直线运动,测得纸带上的点间距,利用匀变速直线运动的推论,可计算出打出某点时纸带运动的瞬时速度和加速度;要知道重物带动纸带下落过程中能量转化的过程和能量守恒.

练习册系列答案
相关题目
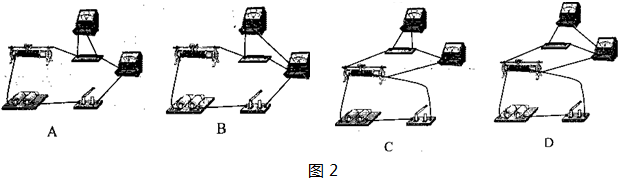
 (2010?成都二模)(1)在验证“机械能守恒定率”的试验中:
(2010?成都二模)(1)在验证“机械能守恒定率”的试验中:
