题目内容
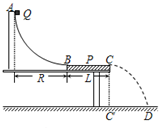 测量小物块Q与平板P之间的动摩擦因数的实验装置如图所示.AB是半径足够大的、光滑的四分之一圆弧轨道,与水平固定放置的P板的上表面BC在B点相切,C点在水平地面的垂直投影为C′.重力加速度为g.实验步骤如下:
测量小物块Q与平板P之间的动摩擦因数的实验装置如图所示.AB是半径足够大的、光滑的四分之一圆弧轨道,与水平固定放置的P板的上表面BC在B点相切,C点在水平地面的垂直投影为C′.重力加速度为g.实验步骤如下:①用天平称出物块Q的质量m;
②测量出轨道AB的半径R、BC的长度L和CC′的高度h;
③将物块Q在A点由静止释放,在物块Q落地处标记其落地点D;
④重复步骤③,共做10次;
⑤将10个落地点用一个尽量小的圆围住,用米尺测量圆心到C′的距离s.
用实验中的测量量表示:
(ⅰ)物块Q到达B点时的动能EkB=
(ⅱ)物块Q到达C点时的动能EkC=
(ⅲ)在物块Q从B运动到C的过程中,物块Q克服摩擦力做的功Wf=
(ⅳ)物块Q与平板P之间的动摩擦因数μ=
分析:(1)物块由A到B点过程,由动能定理可以求出物块到达B时的动能;
(2)物块离开C点后做平抛运动,由平抛运动的知识可以求出物块在C点的速度,然后求出在C点的动能;
(3)由B到C,由动能定理可以求出克服摩擦力所做的功;
(4)由功的计算公式可以求出动摩擦因数.
(2)物块离开C点后做平抛运动,由平抛运动的知识可以求出物块在C点的速度,然后求出在C点的动能;
(3)由B到C,由动能定理可以求出克服摩擦力所做的功;
(4)由功的计算公式可以求出动摩擦因数.
解答:解:(1)从A到B,由动能定理得:mgR=EKB-0,则物块到达B时的动能EKB=mgR;
(2)离开C后,物块做平抛运动,
水平方向:s=vCt,
竖直方向:h=
gt2,
物块在C点的动能EKC=
mvC2,
解得:EKC=
;
(3)由B到C过程中,由动能定理得:
-Wf=
mvC2-
mvB2,
克服摩擦力做的功Wf=mgR-
;
(4)B到C过程中,克服摩擦力做的功:
Wf=μmgL=mgR-
,则μ=
-
;
故答案为:(1)mgR;(2)
;(3)mgR-
;(4)
-
.
(2)离开C后,物块做平抛运动,
水平方向:s=vCt,
竖直方向:h=
| 1 |
| 2 |
物块在C点的动能EKC=
| 1 |
| 2 |
解得:EKC=
| mgs2 |
| 4h |
(3)由B到C过程中,由动能定理得:
-Wf=
| 1 |
| 2 |
| 1 |
| 2 |
克服摩擦力做的功Wf=mgR-
| mgs2 |
| 4h |
(4)B到C过程中,克服摩擦力做的功:
Wf=μmgL=mgR-
| mgs2 |
| 4h |
| R |
| L |
| s2 |
| 4hL |
故答案为:(1)mgR;(2)
| mgs2 |
| 4h |
| mgs2 |
| 4h |
| R |
| L |
| s2 |
| 4hL |
点评:熟练应用动能定理、平抛运动规律、功的计算公式即可正确解题.

练习册系列答案
相关题目
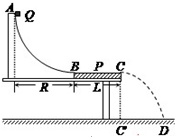 测量小物块Q与平板P之间的动摩擦因数的实验装置如图所示.AB是半径足够大的、光滑的四分之一圆弧轨道,与水平固定放置的P板的上表面BC在B点相切,C点在水平地面的垂直投影为C′.重力加速度为g.实验步骤如下:
测量小物块Q与平板P之间的动摩擦因数的实验装置如图所示.AB是半径足够大的、光滑的四分之一圆弧轨道,与水平固定放置的P板的上表面BC在B点相切,C点在水平地面的垂直投影为C′.重力加速度为g.实验步骤如下:


