题目内容
如图所示,M、N是水平放置的足够长的-平行金属板,两板间接有R=0.3Ω的定值电阻,两板间有垂直于纸面向里的水平匀强磁场,磁感应强度B=0.25T,两板间距d=0.4m.一根总电阻R=0.3Ω的导体棒ab垂直于两金属板紧贴M、N无摩擦地滑动,各处接触电阻均不计.若一个重力不计、带正电荷q=1.6X10-l9C的粒子以v=7m/s的速度水平向右射入M、N两板间,恰能做匀速直线运动,求:(1)ab棒匀速运动的速度;
(2)维持ab棒作匀速直线运动的外力F的功率.

【答案】分析:(1)带正电荷的微粒向右做匀速直线运动,所受的洛伦兹力与电场力平衡,由左手定则判断出洛伦兹力方向,即可知道电场力方向,从而能判断出M、N两板电势的高低,由右手定则判断出ab棒的运动方向.由电荷受力平衡条件列式,求出a、b间的电势差,由闭合电路欧姆定律可求出ab产生的感应电动势E,由E=Bdv求出速度.
(2)维持ab棒作匀速直线运动的外力F的功率等于整个电路的电功率,由公式P= 求解.
求解.
解答:解:(1)由题意,带正电荷的微粒向右做匀速直线运动,所受的洛伦兹力与电场力平衡,由左手定则判断得知洛伦兹力方向竖直向上,则电场力方向竖直向下,可见M板带正电,根据右手定则可以判断出导体棒ab应向右运动.
对电荷:qvB=q
则得 Uab=Bvd
设ab棒匀速运动的速度大小为v,则ab棒切割磁感线产生的感应电动势为 E=Bdv
则有 Uab= =
=
联立以上三式解得 v=14m/s
(2)由ab棒做匀速直线运动,根据功能关系得:F的功率PF=P电=
代入解得PF=3.27W
答:
(1)ab棒匀速运动的速度向右,大小为14m/s;
(2)维持ab棒作匀速直线运动的外力F的功率是3.27W.
点评:本题带电粒子在磁场中运动与电磁感应的综合,它们联系的桥梁是感应电动势,难度不大.
(2)维持ab棒作匀速直线运动的外力F的功率等于整个电路的电功率,由公式P=
 求解.
求解.解答:解:(1)由题意,带正电荷的微粒向右做匀速直线运动,所受的洛伦兹力与电场力平衡,由左手定则判断得知洛伦兹力方向竖直向上,则电场力方向竖直向下,可见M板带正电,根据右手定则可以判断出导体棒ab应向右运动.
对电荷:qvB=q

则得 Uab=Bvd
设ab棒匀速运动的速度大小为v,则ab棒切割磁感线产生的感应电动势为 E=Bdv
则有 Uab=
 =
=
联立以上三式解得 v=14m/s
(2)由ab棒做匀速直线运动,根据功能关系得:F的功率PF=P电=

代入解得PF=3.27W
答:
(1)ab棒匀速运动的速度向右,大小为14m/s;
(2)维持ab棒作匀速直线运动的外力F的功率是3.27W.
点评:本题带电粒子在磁场中运动与电磁感应的综合,它们联系的桥梁是感应电动势,难度不大.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
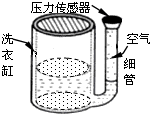 (1)当洗衣缸内水位缓慢升高时,设细管内空气温度不变,
(1)当洗衣缸内水位缓慢升高时,设细管内空气温度不变,
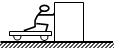 A.男孩和木箱组成的系统动量守恒
A.男孩和木箱组成的系统动量守恒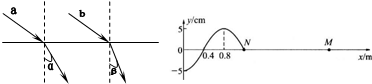



 (1)(5分)如图所示,a、b是两束不同的单色光平行地从空气射入水中,发生折射。α>β,则下列说法正确的是
(1)(5分)如图所示,a、b是两束不同的单色光平行地从空气射入水中,发生折射。α>β,则下列说法正确的是 