题目内容
（1）如图，一个三棱镜的截面为等腰直角△ABC，∠A为直角．此截面所在平面内的光线沿平行于BC边的方向射到AB边，进入棱镜后直接射到AC边上，并刚好能发生全反射．该棱镜材料的折射率为 ．（填入正确选项前的字母）
A.
B.
C.
D.
（2）波源S1和S2振动方向相同，频率均为4Hz，分别置于均匀介质中x轴上的O、A两点处，OA=2m，如图所示．两波源产生的简谐横波沿x轴相向传播，波速为4m/s．己知两波源振动的初始相位相同．求：
（i）简谐横波的波长：
（ii）OA间合振动振幅最小的点的位置．
A.
| ||
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
（2）波源S1和S2振动方向相同，频率均为4Hz，分别置于均匀介质中x轴上的O、A两点处，OA=2m，如图所示．两波源产生的简谐横波沿x轴相向传播，波速为4m/s．己知两波源振动的初始相位相同．求：
（i）简谐横波的波长：
（ii）OA间合振动振幅最小的点的位置．
分析：（1）由题意可知各角的大小，则由折射定律及全反射可得出角与折射率的关系，联立可求得折射率；
（2）已知频率及波速，则由波速公式可求得波长；
要使振动振幅最小，则该点到两波源的波程差应为半波长的奇数倍，设距O点为x，则可得出波程差的表达式，联立可解得位置．
（2）已知频率及波速，则由波速公式可求得波长；
要使振动振幅最小，则该点到两波源的波程差应为半波长的奇数倍，设距O点为x，则可得出波程差的表达式，联立可解得位置．
解答：解：如图所示，根据折射率定义有，sin∠1=nsin∠2，nsin∠3=1，已知∠1=45°∠2+∠3=90°，
联立解得：n=
故选A；
（2）（i）设波长为λ，频率为ν，则v=λν，代入已知数据得：λ=1m；
（ii）以O为坐标原点，设P为OA间任一点，其坐标为x，则两波源到P点的波程差△l=x-（2-x），
0≤x≤2．其中x、△l以m为单位．
合振动振幅最小的点的位置满足△l=(k+
)λ，k为整数
则可解得：x=0.25m．0.75m，1.25m，1.75m．
故最小点的位置可以为0.25m，0.75m，1.25m，1.75m．
联立解得：n=
| ||
| 2 |
故选A；
（2）（i）设波长为λ，频率为ν，则v=λν，代入已知数据得：λ=1m；
（ii）以O为坐标原点，设P为OA间任一点，其坐标为x，则两波源到P点的波程差△l=x-（2-x），
0≤x≤2．其中x、△l以m为单位．
合振动振幅最小的点的位置满足△l=(k+
| 1 |
| 2 |
则可解得：x=0.25m．0.75m，1.25m，1.75m．
故最小点的位置可以为0.25m，0.75m，1.25m，1.75m．
点评：第一小题的关键在于利用几何关系找出入射角、折射角及反射角，由折射定律可列出方程；
第二小题在于理解振幅最小的点应满足光程差相差半波长的奇数倍，再由数学关系可求得可能出现的位置，同时要明确本题具有多解性．
第二小题在于理解振幅最小的点应满足光程差相差半波长的奇数倍，再由数学关系可求得可能出现的位置，同时要明确本题具有多解性．
练习册系列答案
相关题目
如图所示，一个用透明材料制成的截面为直角三角形的三棱ABC，现在有一束单色光从空气中以θ1=45°的入射角自直角边 AB射入，折射时的偏向角为15°，然后光线射到AC面时刚好发生了全反射．求：
如图所示，是一个用折射率，n=1.6的透明介质做成的三棱柱的横截面图，其中∠A=60°，∠C=30°．现有一条光线从图中所示的位置垂直入射到棱镜的AB面上．试求：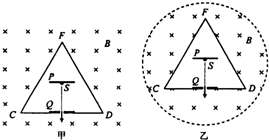
如图甲所示，在空心三棱柱CDF以外足够大的空间中，充满着磁感应强度为B的匀强磁场．三棱柱的轴线与磁场平行，截面边长为L，三棱柱用绝缘薄板材料制成，其内部有平行于CD侧面的金属板P、Q，两金属板间的距离为d，P板带正电，Q板带负电，Q板中心有一小孔，P板上与小孔正对的位置有一个粒子源S，从S处可以发出初速度为0、带电量为+q、质量为m的粒子，这些粒子与三棱柱侧面碰撞时无能量损失．试求：
