题目内容
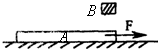 如图所示,质量显m1=2kg的木板A放在水平面上,木板与水平面间的动摩擦因数为μ1=0.1.木板在F=7N的水平拉力作用下由静止开始向右做匀加速运动,经过时间t=4s时在木板的右端轻放一个质量为m2=1kg的木块B,木块与木板间的动摩擦因数为μ2=0.4.且木块可以看成质点.若要使木块不从木板上滑下来,求木板的最小长度.
如图所示,质量显m1=2kg的木板A放在水平面上,木板与水平面间的动摩擦因数为μ1=0.1.木板在F=7N的水平拉力作用下由静止开始向右做匀加速运动,经过时间t=4s时在木板的右端轻放一个质量为m2=1kg的木块B,木块与木板间的动摩擦因数为μ2=0.4.且木块可以看成质点.若要使木块不从木板上滑下来,求木板的最小长度.分析:根据牛顿第二定律和速度时间公式求出放上木块B前木板的速度,再根据 牛顿第二定律求出放上木块后木板的加速度以及木块的加速度,抓住两者速度相同,恰好不滑下,结合运动学公式求出木板的最小长度.
解答:解:开始时木板的加速度为:
a=
=
=2.5m/s2
t秒末木板的速度为:
v=at=2.5×4m/s=10m/s
放上木块后木板的加速度为:
a1=
=
=0
木块的加速度为:
a2=μ2g=0.4×10=4m/s2
可见t秒后木板做匀速运动,木块做匀加速运动,当木块不从木板上滑下时,两者具有相同的速度.
设木块加速到木板的速度时所用的时间为t′则:
t′=
=
=2.5s.
这段时间内木块相对于木板滑动的距离为:
L=vt′-
a2t′2=10×2.5-
×4×2.52=12.5m
答:木板的最小长度为12.5m.
a=
| F-μ1m1g |
| m1 |
| 7-0.1×20 |
| 2 |
t秒末木板的速度为:
v=at=2.5×4m/s=10m/s
放上木块后木板的加速度为:
a1=
| F-μ1(m1+m2)g-μ2m2g |
| m1 |
| 7-0.1×30-0.4×10 |
| 2 |
木块的加速度为:
a2=μ2g=0.4×10=4m/s2
可见t秒后木板做匀速运动,木块做匀加速运动,当木块不从木板上滑下时,两者具有相同的速度.
设木块加速到木板的速度时所用的时间为t′则:
t′=
| v |
| a2 |
| 10 |
| 4 |
这段时间内木块相对于木板滑动的距离为:
L=vt′-
| 1 |
| 2 |
| 1 |
| 2 |
答:木板的最小长度为12.5m.
点评:本题考查了牛顿第二定律和运动学公式的综合运用,关键理清放上木块后木板和木块的运动情况,抓住临界状态,结合牛顿第二定律和运动学公式进行求解.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
 如图所示,质量显m1=2kg的木板A放在水平面上,木板与水平面间的动摩擦因数为μ1=0.1.木板在F=7N的水平拉力作用下由静止开始向右做匀加速运动,经过时间t=4s时在木板的右端轻放一个质量为m2=1kg的木块B,木块与木板间的动摩擦因数为μ2=0.4.且木块可以看成质点.求:
如图所示,质量显m1=2kg的木板A放在水平面上,木板与水平面间的动摩擦因数为μ1=0.1.木板在F=7N的水平拉力作用下由静止开始向右做匀加速运动,经过时间t=4s时在木板的右端轻放一个质量为m2=1kg的木块B,木块与木板间的动摩擦因数为μ2=0.4.且木块可以看成质点.求: (1)下列说法正确的有
(1)下列说法正确的有


 如图所示,质量显m1=2kg的木板A放在水平面上,木板与水平面间的动摩擦因数为μ1=0.1.木板在F=7N的水平拉力作用下由静止开始向右做匀加速运动,经过时间t=4s时在木板的右端轻放一个质量为m2=1kg的木块B,木块与木板间的动摩擦因数为μ2=0.4.且木块可以看成质点.求:
如图所示,质量显m1=2kg的木板A放在水平面上,木板与水平面间的动摩擦因数为μ1=0.1.木板在F=7N的水平拉力作用下由静止开始向右做匀加速运动,经过时间t=4s时在木板的右端轻放一个质量为m2=1kg的木块B,木块与木板间的动摩擦因数为μ2=0.4.且木块可以看成质点.求: