题目内容
如图所示，一滑块从半圆形光滑轨道上端由静止开始滑下，当滑到最低点时，关于滑块动能大小和对轨道最低点的压力，下列结论正确的是（ ）分析：根据动能定理得出小球运动到最低点的速度，根据牛顿第二定律求出最低点轨道对小球的支持力，从而得到球对轨道底端压力的大小与半径的关系．
解答：解：对于物体下滑的过程，根据动能定理得：mgR=
mv2，v2=2gR．
物体到达最低点的动能为EK=
mv2=mgR，可见，质量越大，半径越大，动能越大．
在轨道最低点，由牛顿第二定律得，N-mg=m
，解得N=3mg．则知A、B两球对轨道的压力大小与半径也无关，只与重力有关．
故A错误，B正确，C错误，D正确；
故选BD．
| 1 |
| 2 |
物体到达最低点的动能为EK=
| 1 |
| 2 |
在轨道最低点，由牛顿第二定律得，N-mg=m
| v2 |
| R |
故A错误，B正确，C错误，D正确；
故选BD．
点评：本题综合考查了动能定理和牛顿第二定律，关键掌握向心力的来源．本题中的结果要作为常识记住．
练习册系列答案
相关题目
将一个力传感器连接到计算机上，我们就可以测量快速变化的力．如图所示就是用这种方法测得的小滑块在半球形碗内在竖直平面内来回滑动时，对碗的压力大小随时间变化的曲线．从这条曲线提供的信息，可以判断滑块约每隔
如图所示，ABCDE是由三部分光滑轨道平滑连接在一起组成的，AB为水平轨道，
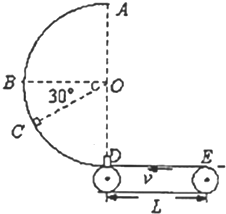如图所示，传送带以v为7
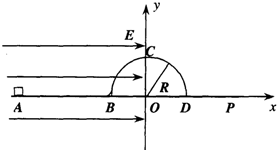如图所示，光滑水平面上固定着一半径为R的光滑半圆柱体，半圆柱体的轴线过坐标原点O，在x＜0 一侧的整个空间存在电场强度大小为E、方向水平向右的匀强电场一个质量为m、带正电荷q的小滑块，从水平面上的A点由静止释放，到达B点后沿半圆柱面继续上滑（B点处有一光滑小圆弧面连接水平面与半圆柱面），达到半圆柱面顶点C时，小滑块对半圆柱面的压力恰好为零，离开柱面后小滑块落到水平上的P点．试求：
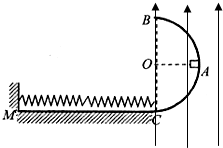如图所示，光滑半圆弧绝缘轨道半径为R，OA为水平半径，BC为竖直直径．一质量为m且始终带+q电量的小物块自A处以某一竖直向下的初速度滑下，进入与C点相切的粗糙水平绝缘滑道CM上，在水平滑道上有一轻弹簧，其一端固定在竖直墙上，另一端恰位于滑道的末端C点，此时弹簧处于自然状态．物块运动过程中弹簧最大弹性势能为EP，物块被弹簧反弹后恰能通过B点．己知物块与水平滑道间的动摩擦因数为μ，直径BC右侧所处的空间（包括BC边界）有竖直向上的匀强电场，且电场力为重力的一半．求：