题目内容
小船在静水中的速度是6m/s,河水的流速是3m/s,河宽60m,小船渡河时,船头指向与河岸垂直,它将在正对岸的 游 m处靠岸,过河时间t= s.如果要使实际航线与河岸垂直,船头应指向河流的上游,与河岸所成夹角α= .
【答案】分析:将小船的运动分解为沿河岸方向和垂直于河岸方向,抓住分运动与合运动具有等时性,求出到达对岸沿水流方向上的位移以及时间.
当实际航线与河岸垂直,则合速度的方向垂直于河岸,根据平行四边形定则求出船头与河岸所成的夹角.
解答:解:渡河时间t=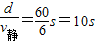 ,则沿河岸方向上的位移x=v水t=3×10m=30m,所以船将在正对岸下游30m处靠岸.
,则沿河岸方向上的位移x=v水t=3×10m=30m,所以船将在正对岸下游30m处靠岸.
当实际航线与河岸垂直,则合速度的方向垂直于河岸,根据平行四边形定则有:cos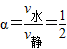 ,所以α=60°.
,所以α=60°.
故答案为:下,30m,10,60°.
点评:解决本题的关键知道分运动和合运动具有等时性,以及会根据平行四边形定则对运动进行合成和分解.
当实际航线与河岸垂直,则合速度的方向垂直于河岸,根据平行四边形定则求出船头与河岸所成的夹角.
解答:解:渡河时间t=
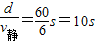 ,则沿河岸方向上的位移x=v水t=3×10m=30m,所以船将在正对岸下游30m处靠岸.
,则沿河岸方向上的位移x=v水t=3×10m=30m,所以船将在正对岸下游30m处靠岸.当实际航线与河岸垂直,则合速度的方向垂直于河岸,根据平行四边形定则有:cos
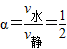 ,所以α=60°.
,所以α=60°.故答案为:下,30m,10,60°.
点评:解决本题的关键知道分运动和合运动具有等时性,以及会根据平行四边形定则对运动进行合成和分解.

练习册系列答案
相关题目
小船在静水中的速度是2m/s,水流速度是
m/s,当调整船头方向,使其与河岸所夹的角度为θ(θ<90°)时,船可以用最短位移过河,则θ角应为( )
| 3 |
| A、90° | B、60° |
| C、30° | D、120° |