题目内容
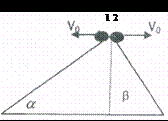
 两个同高度斜面,倾角分别为α、β,小球1、2分别由斜面顶端以相等水平速度抛出,如图所示,假设两球能落在斜面上,则小球1、2飞行下落的高度之比为( )
两个同高度斜面,倾角分别为α、β,小球1、2分别由斜面顶端以相等水平速度抛出,如图所示,假设两球能落在斜面上,则小球1、2飞行下落的高度之比为( )分析:两个小球均做平抛运动,根据斜面倾角的正切等于竖直位移与水平位移之比求出运动时间,再由竖直方向小球做自由落体运动,求出高度,再求解高度之比.
解答:解:设两球平抛运动的初速度为v0,则
对于球1:tanα=
=
=
,得到运动时间t1=2
,下落高度h1=
g
同理,得到球2运动时间t2=2
,下落高度h2=
g
则得到h1:h2=tan2α:tan2β
故选D
对于球1:tanα=
| h |
| x |
| ||||
| v0t1 |
| gt1 |
| 2v0 |
| v0tanα |
| g |
| 1 |
| 2 |
| t | 2 1 |
同理,得到球2运动时间t2=2
| v0tanβ |
| g |
| 1 |
| 2 |
| t | 2 2 |
则得到h1:h2=tan2α:tan2β
故选D
点评:本题是有条件的平抛运动,关键是斜面倾角的运用.要注意斜面倾角的正切等于竖直位移与水平位移之比,不等于竖直方向速度与水平方向速度之比.

练习册系列答案
相关题目