题目内容
(8分)质量为M的小车置于水平面上,小车的上表面由光滑的1/4圆弧和光滑平面组成,圆弧半径为R,车的右端固定一轻弹簧,如图所示.现将一质量为m的滑块从圆弧最高处无初速下滑,与弹簧相接触并压缩弹簧.求:

①弹簧具有的最大弹性势能Ep.
②当滑块与弹簧分离时小车的速度v.
【答案】
①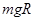 ②
②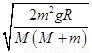
【解析】
试题分析:①滑块与小车相互作用过程中水平方向动量守恒,系统水平方向的总动量始终为0,滑块压缩弹簧后,当二者速度相等时,弹簧弹性势能最大,此时小车与滑块的速度均为零.
由机械能守恒定律得,弹簧最大弹性势能为: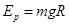
②设滑块与弹簧分离时,滑块的速度为v′,由系统动量守恒得:
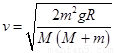
由机械能守恒定律得:
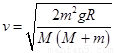
联立两式解得小车的速度: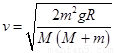
考点:本题综合考查了动量守恒定律和能量守恒定律,同时考查考生应用动量观点和能量观点解决碰撞问题的能力.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目





 ,
, ,
, ,
, ,
, ,
,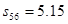 cm。试问:
cm。试问:
 = m/s(结果保留2位有效数字);若滴水的周期为T,则小车的加速度
= m/s(结果保留2位有效数字);若滴水的周期为T,则小车的加速度 =
(用英文符号表示)。
=
(用英文符号表示)。




 、
、 ,并测出间距d 。开始时让木板置于
,并测出间距d 。开始时让木板置于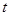 。
。
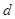 、
、 = ;为了减小测量加速度的偶然误差可以采用的方法是(一种即可) 。
= ;为了减小测量加速度的偶然误差可以采用的方法是(一种即可) 。 