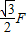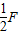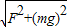题目内容
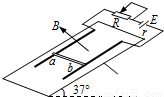
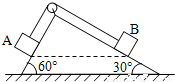
在倾角为60°的光滑斜面上，一小球从A点由静止释放经时间t到达B点；另一个小球从A点水平抛出，落点也在B点，重力加速度为g，可知平抛小球在空中运动时间为 ，平抛小球的初速度为 ．
【答案】分析：根据牛顿第二定律求出小球从斜面滑下的加速度，由位移求出A到B的位移大小．根据两球的位移相同，则可求出另一小球下落的高度．根据平抛运动竖直方向是自由落体运动，由高度求出时间．由水平方向的匀速运动，求出初速度．
解答：解：设A到B的距离为S．
小球从斜面滑下的加速度大小为a=gsin60°，S=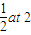
=
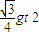
对于平抛运动的小球，设运动时间为t，则
Ssin60°=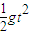
代入解得 t=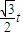
初速度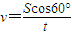
=
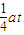
故答案为：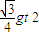
，
．
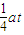点评：本题首先要抓住两个运动的关系：位移相同，其次抓住平抛运动的研究方法：运动的分解．
解答：解：设A到B的距离为S．
小球从斜面滑下的加速度大小为a=gsin60°，S=
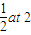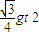
=对于平抛运动的小球，设运动时间为t，则
Ssin60°=
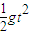
代入解得 t=
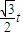
初速度
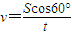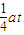
=故答案为：
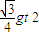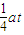，．点评：本题首先要抓住两个运动的关系：位移相同，其次抓住平抛运动的研究方法：运动的分解．
练习册系列答案
口算题天天练系列答案
相关题目
