题目内容
如图所示,M是一块平面镜,位于透明液体之中,镜面水平向上放置,一细束光线a竖直向下射来,穿过液体射到平面镜上,现将平面镜绕水平轴在竖直面内顺时针转动15°角,光线经平面镜反射后在液面处分成两束,这两束光线恰好垂直,求;(1)求该液体的折射率.
(2)若使光线经平面镜反射后在液面处恰好发生全反射,平面镜由初始水平位置绕水平轴在竖直面内顺时针转过的最小角度(用三角函数表示).
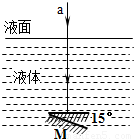
【答案】分析:(1)将平面镜绕水平轴顺时针转过15°角,反射光线将顺时针转过30°,反射光线在液面处的入射角等于30°,而反射光在液面处形成的反射光与折射光垂直,画出光路图,根据几何知识求出入射角为i=30°,折射角为r=60°,则可公式n=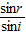 求出折射率n.
求出折射率n.
(2)若使光线经平面镜反射后在液面处恰好发生全反射,入射角必须等于临界角.由公式sinC=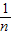 求出临界角,再根据平面镜的光学特点求出平面镜转过的角度.
求出临界角,再根据平面镜的光学特点求出平面镜转过的角度.
解答:解:(1)将平面镜绕水平轴顺时针转过15°角,反射光线将顺时针转过30°,反射光线在液面处的入射角i=30°,如图所示.
由题意,反射光在液面处形成的反射光与折射光垂直,根据几何知识得:折射角为r=60°,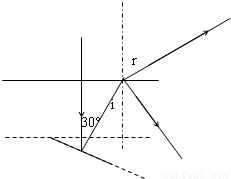
故折射率n=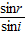 =
=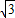 .
.
(2)设临界角为C,则sinC=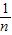 =
=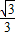
则得C=arcsin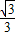
若使光线经平面镜反射后在液面处恰好发生全反射,入射角必须等于临界角,说明反射光线转过了C角.
根据平面镜的光学特点可知,平面镜顺时针转过的最小角度为α= C=
C= arcsin
arcsin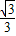 .
.
答:(1)该液体的折射率为n=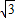 .
.
(2)若使光线经平面镜反射后在液面处恰好发生全反射,平面镜由初始水平位置绕水平轴在竖直面内顺时针转过的最小角度为 arcsin
arcsin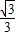 .
.
点评:画出光路图是解决几何光学问题的基础,本题要充分运用平面镜的光学特征和几何知识研究出入射角和折射角,就能轻松解答.
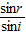 求出折射率n.
求出折射率n.(2)若使光线经平面镜反射后在液面处恰好发生全反射,入射角必须等于临界角.由公式sinC=
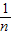 求出临界角,再根据平面镜的光学特点求出平面镜转过的角度.
求出临界角,再根据平面镜的光学特点求出平面镜转过的角度.解答:解:(1)将平面镜绕水平轴顺时针转过15°角,反射光线将顺时针转过30°,反射光线在液面处的入射角i=30°,如图所示.
由题意,反射光在液面处形成的反射光与折射光垂直,根据几何知识得:折射角为r=60°,

故折射率n=
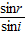 =
=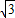 .
.(2)设临界角为C,则sinC=
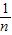 =
=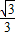
则得C=arcsin
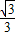
若使光线经平面镜反射后在液面处恰好发生全反射,入射角必须等于临界角,说明反射光线转过了C角.
根据平面镜的光学特点可知,平面镜顺时针转过的最小角度为α=
 C=
C= arcsin
arcsin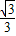 .
.答:(1)该液体的折射率为n=
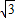 .
.(2)若使光线经平面镜反射后在液面处恰好发生全反射,平面镜由初始水平位置绕水平轴在竖直面内顺时针转过的最小角度为
 arcsin
arcsin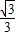 .
.点评:画出光路图是解决几何光学问题的基础,本题要充分运用平面镜的光学特征和几何知识研究出入射角和折射角,就能轻松解答.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
 如图所示,利用静电计研究平行板电容器的电容与哪些因素有关.实验过程中,平行板上的电量可认为不变.下列叙述中正确的是( )
如图所示,利用静电计研究平行板电容器的电容与哪些因素有关.实验过程中,平行板上的电量可认为不变.下列叙述中正确的是( )



