题目内容
如图所示,a、b、c,是地球大气层外圆形轨道上运动的三颗卫星,a和
b的质量相等且小于c的质量,则
[ ]
A.b所需向心力最小
B.b、c的周期相等且大于a的周期
C.b、c的向心加速度大小相等,且大于a的向心加速度
D.b、c的线速度大小相等,且小于a的线速度

答案:ABD
解析:
解析:
|
因卫星运动的向心力就是它们所受的万有引力,而 b所受的引力最小,故A对.由 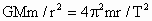 ,得 ,得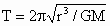 ,即人造地球卫星运行周期与其轨道半径三次方的平方根成正比,所以b、c,的周期相等且大于a的周期.B项对. ,即人造地球卫星运行周期与其轨道半径三次方的平方根成正比,所以b、c,的周期相等且大于a的周期.B项对.
由 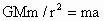 得 得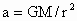 ,即卫星的向心加速度与轨道半径的平方成反比.所以b、c的向心加速度大小相等且小于a的向心加速度.故C项错. ,即卫星的向心加速度与轨道半径的平方成反比.所以b、c的向心加速度大小相等且小于a的向心加速度.故C项错.
由 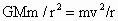 得 得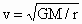 ,即地球卫星的线速度与其轨道半径的平方根成反比,所以b、c线速度大小相等且小于a的线速度,D项对. ,即地球卫星的线速度与其轨道半径的平方根成反比,所以b、c线速度大小相等且小于a的线速度,D项对.
(1) 人造卫星的运动都可以近似看作匀速圆周运动,其向心力就是地球对它的万有引力,设卫星的质量为m,围绕地球做匀速圆周运动的半径为r,线速度为v,地球的质量为M,则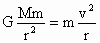 ,解得 ,解得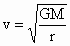 ,此式即为人造地球卫星环绕地球运行线速度大小的表达式,由表达式可以看出,轨道半径r越大,环绕速度v越小. ,此式即为人造地球卫星环绕地球运行线速度大小的表达式,由表达式可以看出,轨道半径r越大,环绕速度v越小.
(2) 卫星做匀速圆周运动的各物理量随轨道半径的变化而变化的规律主体方程的等号左边是万有引力的计算式,主体方程的等号的右边是向心力的计算式. ①向心力和向心加速度:向心力是由万有引力充当的,有 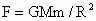 .再据F=ma,必然有: .再据F=ma,必然有: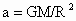 .所以有:随着卫星轨道半径的增加,做匀速圆周运动的卫星的向心力和向心加速度皆减小. .所以有:随着卫星轨道半径的增加,做匀速圆周运动的卫星的向心力和向心加速度皆减小.
②线速度 v:依据主体方程有: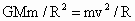 所以, 所以,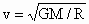 . .
所以有:随着轨道半径的增加,做匀速圆周运动的卫星的线速度减小.即 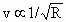
(3) 角速度ω:依据主体方程有: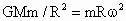 ,所以, ,所以,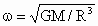 . .
所以有:随着轨道半径的增加,做匀速圆周运动的卫星的角速度减小.即 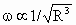 . .
(4) 周期T:依据主体方程有: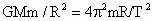 , ,
所以, 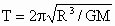 . .
所以有:随着轨道半径的增加,做匀速圆周运动的卫星的周期增大.即 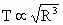 . .
由以上分析可知:在进行本类题目的计算和判断时,应特别注意:主体方程的等号左边一定写成 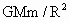 .等号右边一定注意讨论哪个物理量,就要用哪个物理量所表达的向心力公式,例如讨论线速度就写成 .等号右边一定注意讨论哪个物理量,就要用哪个物理量所表达的向心力公式,例如讨论线速度就写成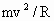 另外也可以看出,卫星的线速度v、角速度ω、周期T、加速度a等皆与卫星的质量无关,只由R和M决定. 另外也可以看出,卫星的线速度v、角速度ω、周期T、加速度a等皆与卫星的质量无关,只由R和M决定. |

练习册系列答案
相关题目

 如图所示,a、b、c为电场中同一电场线上的三点,且b为ac的中点,a、c电势分别为φa=8V,φc=6V.下列叙述正确的是( )
如图所示,a、b、c为电场中同一电场线上的三点,且b为ac的中点,a、c电势分别为φa=8V,φc=6V.下列叙述正确的是( ) 如图所示,A、B、C、D是某匀强电场中的4个等势面,一个质子和一个α粒子(电荷量是质子的2倍,质量是质子的4倍)同时在A等势面从静止出发,向右运动,当到达D等势面时,下列说法正确的是( )
如图所示,A、B、C、D是某匀强电场中的4个等势面,一个质子和一个α粒子(电荷量是质子的2倍,质量是质子的4倍)同时在A等势面从静止出发,向右运动,当到达D等势面时,下列说法正确的是( ) 如图所示,a、b和c都是厚度均匀的平玻璃板,a和b、b和c之间的夹角都为α,一细光束由红光和蓝光组成,以入射角θ从O点射入a板,且射出c板后的两束单色光通过空气射在地面上P、Q两点,由此可知( )
如图所示,a、b和c都是厚度均匀的平玻璃板,a和b、b和c之间的夹角都为α,一细光束由红光和蓝光组成,以入射角θ从O点射入a板,且射出c板后的两束单色光通过空气射在地面上P、Q两点,由此可知( )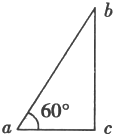 如图所示,a、b、c是匀强电场中的直角三角形的三个顶点.已知a、b、c三点的电势分别为φa=8V、φb=-4V、φc=2V,
如图所示,a、b、c是匀强电场中的直角三角形的三个顶点.已知a、b、c三点的电势分别为φa=8V、φb=-4V、φc=2V,