Question

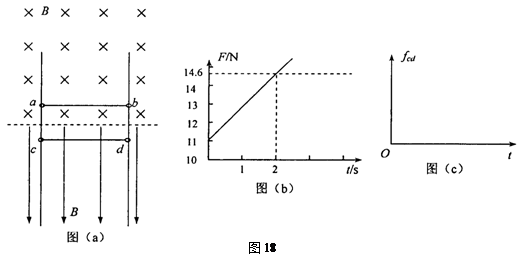
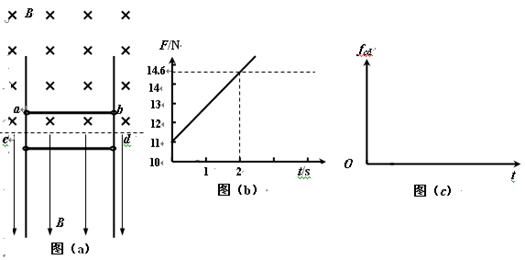
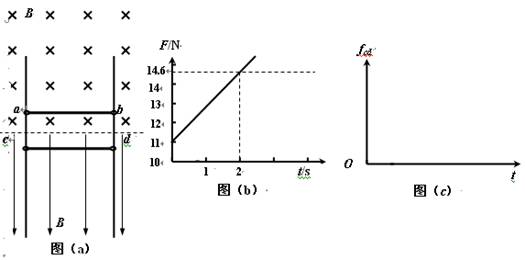
相距L＝1.5m的足够长金属导轨竖直放置，质量为m₁＝1kg的金属棒ab和质量为m₂＝0.27kg的金属棒cd均通过棒两端的套环水平地套在金属导轨上，如图（a）所示，虚线上方磁场方向垂直纸面向里，虚线下方磁场方向竖直向下，两处磁场磁感应强度大小相同。ab棒光滑，cd棒与导轨间动摩擦因数为μ＝0.75，两棒总电阻为1.8Ω，导轨电阻不计。ab棒在方向竖直向上，大小按图（b）所示规律变化的外力F作用下，从静止开始，沿导轨匀加速运动，同时cd棒也由静止释放。(g=10m/S²)

（1）求出磁感应强度B的大小和ab棒加速度大小；

（2）已知在2s内外力F做功40J，求这一过程中两金属棒产生的总焦耳热；

（3）求出cd棒达到最大速度所需的时间t₀，并在图（c）中定性画出cd棒所受摩擦力f_cd随时间变化的

Answer 1

（1）经过时间t，金属棒ab的速率                                                        (1分)

此时，回路中的感应电流为                                 (2分)

对金属棒ab，由牛顿第二定律得        

由以上各式整理得：                                      (2分）

      在图线上取两点：              t₁=0，F₁=11N； t₂=2s，F₂=14．6N

代入上式得                                          B＝1．2T                               （2分）

   （2）在2s末金属棒ab的速率                                 (1分)

所发生的位移                                                               (1分)

       由动能定律得                                                   （2分）

又                                                                  (1分)                                                                   

联立以上方程，解得

                         (2分)

（3）cd棒先做加速度逐渐减小的加速运动，当cd棒所受重力与滑动摩擦力相等时，速度达到最大；然后做加速度逐渐增大的减速运动，最后停止运动。      

当cd棒速度达到最大时，对cd棒有：               

又                                                                           

                   整理解得                               （ 2分）

    对abcd回路：                        

           解得                  （2分）

                 得   t₀=2s                                                （1分）

f_cd随时间变化的图象如图（c）所示。     （3分）（若无体现2秒值，其他都正确的，不扣分；若无体现末态静止，扣除1分；若无体现动摩擦到静摩擦的大小突变小，扣除1分；若动摩擦没体现线性增大，不给分）