题目内容
如图所示，一块质量为
M＝2 kg，长L＝1 m的匀质木板放在足够长的水平桌面上，初始时速度为零．板的最左端放置一个质量m＝1 kg的小物块，小物块与木板间的动摩擦因数为μ1＝0.2，小物块上连接一根足够长的水平轻质细绳，细绳跨过位于桌面边缘的定滑轮(细绳与滑轮间的摩擦不计，木板与滑轮之间距离足够长，g＝10 m/s2)，要求：
(
1)若木板被固定，恒力F＝4 N向下拉绳，求小木块滑离木板时的速度大小v1；(
2)若不固定木板，且板与桌面间光滑，某人仍以恒力F＝4 N向下拉绳，求小木块滑离木板时的速度大小v2；(
3)若不固定木板，若板与桌面间有摩擦，某人以恒定速度v＝1 m/s向下拉绳，为使物块能从板的右端滑出，求板与桌面间的动摩擦因数μ2．
答案：
解析：
解析：
|
(1)对小物块受力分析 由牛顿第二定律： 得：a＝2 m/s2(1分) 运动学公式： 得：v1＝2 m/s(1分) (2)对小物块、木板受力分析 由牛顿第二定律： 得：a1＝2 m/s2(1分) 由： 得：a2＝2 m/s2(1分) 物块的位移： 木板的位移： 又：x2－x1＝L(1分) 解得： 得： (3)设物块在板上滑行的时间为t，物块滑到木板右端时的速度大小刚好为v，板与桌面间的动摩擦因数μ0． 对木板： 对物块： 解得： 得： 为了使物块能从板的右端滑出， |
，
(1分)
(1分)
(1分)
(1分)
(1分)
(1分)
(1分)
练习册系列答案
智能训练练测考系列答案
计算高手系列答案
相关题目
如图所示，一块质量为M，长为L的均质长木板放在很长的光滑水平桌面上，板的左端有一质量为m的小物体（可视为质点），物体上连接一根很长的细绳，细绳跨过位于桌边的定滑轮．某人以恒定的速率v向下拉绳，物体最多只能到达板的中点，已知整个过程板的右端都不会到达桌边定滑轮处．试求：
如图所示，一块质量为M的木板停在光滑的水平面上，木板的左端有挡板，挡板上固定一个小弹簧．一个质量为m的小物块（可视为质点）以水平速度υ0从木板的右端开始向左运动，与弹簧碰撞后（弹簧处于弹性限度内），最终又恰好停在木板的右端．根据上述情景和已知量，可以求出四个物理量中的（ ）
（2006?淮安模拟）如图所示，一块质量为2kg、涂有碳黑的玻璃板，在拉力F的作用下竖直向上做匀变速直线运动．一个频率为5Hz的振动方向为水平且固定的振针，在玻璃板上画出了如图所示的图线，量得OA=1cm，OB=4cm，OC=9cm．求拉力F的大小．（不计一切摩擦阻力，取g=10m/s2）
（2012?泸州一模）如图所示，一块质量为M的木板停在光滑的水平面上，木板的左端有挡板，挡板上固定一个小弹簧．一个质量为m的小物块（可视为质点）以水平速度υ0从木板的右端开始向左运动，与弹簧碰撞后（弹簧处于弹性限度内），最终又恰好停在木板的右端．根据上述情景和已知量，可以求出（ ）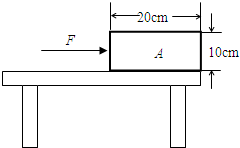
如图所示，一块质量为m=15kg，长为20cm、高为10cm的均匀长方体物块A，静置于水平桌面上，其右端与桌边平齐，物块A与桌面之间的动摩擦因数为?=0.4（设最大静摩擦力与滑动摩擦力大小相同），现在物块A高度的1/2处施加一水平推力F，则推动这一物块所需的最小推力大小为