题目内容
 如图所示,在空间有一坐标系xOy,直线OP与轴正方向的夹角为30°,第一象限内有两个方向都垂直纸面向外的匀强磁场区域I和II,直线OP上方区域I中磁场的磁感应强度为B.一质量为m,电荷量为q的质子(不计重力)以速度v从O点沿与OP成30°角的方向垂直磁场进入区域I,质子先后通过强磁场区域I和II后,恰好垂直打在x轴上的Q点(图中未画出),则 ( )
如图所示,在空间有一坐标系xOy,直线OP与轴正方向的夹角为30°,第一象限内有两个方向都垂直纸面向外的匀强磁场区域I和II,直线OP上方区域I中磁场的磁感应强度为B.一质量为m,电荷量为q的质子(不计重力)以速度v从O点沿与OP成30°角的方向垂直磁场进入区域I,质子先后通过强磁场区域I和II后,恰好垂直打在x轴上的Q点(图中未画出),则 ( )分析:(1)质子在两个磁场中由洛伦兹力提供向心力,均做匀速圆周运动.根据圆的对称性可知,质子从A点出磁场I时的速度方向与OP的夹角为30°,即与x轴平行.在区域II中,由题分析可知,质子运动
圆周,由几何知识作出轨迹,如图.由几何关系,得到质子在两个磁场中轨迹半径与OA的关系,由牛顿第二定律研究两个磁感应强度的关系,求解区域II中磁场的磁感应强度大小.
然后结合带电粒子在磁场中运动的时间与转过的角度的关系:
=
求出质子先后通过强磁场区域I和II的时间,总时间即为所求;
(2)由图x=OAcos30°+r2=r1cos30°+r2求解x.
| 1 |
| 4 |
然后结合带电粒子在磁场中运动的时间与转过的角度的关系:
| θ |
| 360° |
| t |
| T |
(2)由图x=OAcos30°+r2=r1cos30°+r2求解x.
解答:解: (1)设质子在磁场I和II中做圆周运动的轨道半径分别为r1和r2,区域II中磁感应强度为B′,
(1)设质子在磁场I和II中做圆周运动的轨道半径分别为r1和r2,区域II中磁感应强度为B′,
由牛顿第二定律qvB=m
①
qvB′=m
②
粒子在两区域运动的轨迹如图所示,由带电粒子才磁场中运动的对称性和几何关系可知,质子从A点出磁场I时的速度方向与OP的夹角为30°,故质子在磁场I中轨迹的圆心角为 θ=60°,如图:
则△O1OA为等边三角形 OA=r1 ③
在区域II中,质子运动
圆周,O2是粒子在区域II中做圆周运动的圆心,r2=OAsin30°④
由①②③④解得区域II中磁感应强度为 B′=2B ⑤
粒子在Ⅰ区的运动周期:T1=
,
=
⑥
粒子在Ⅱ区运动的周期:T2=
,
=
⑦
粒子在第一象限中运动的时间为:t=t1+t2 ⑧
联立⑤⑥⑦⑧解得:t=
故选项A正确.选项B错误;
(2)Q点坐标 x=OAcos30°+r2=r1cos30°+r2
代人数据得:x=
故选项C正确,D错误.
故选:AC
 (1)设质子在磁场I和II中做圆周运动的轨道半径分别为r1和r2,区域II中磁感应强度为B′,
(1)设质子在磁场I和II中做圆周运动的轨道半径分别为r1和r2,区域II中磁感应强度为B′,由牛顿第二定律qvB=m
| v2 |
| r1 |
qvB′=m
| v2 |
| r2 |
粒子在两区域运动的轨迹如图所示,由带电粒子才磁场中运动的对称性和几何关系可知,质子从A点出磁场I时的速度方向与OP的夹角为30°,故质子在磁场I中轨迹的圆心角为 θ=60°,如图:
则△O1OA为等边三角形 OA=r1 ③
在区域II中,质子运动
| 1 |
| 4 |
由①②③④解得区域II中磁感应强度为 B′=2B ⑤
粒子在Ⅰ区的运动周期:T1=
| 2πm |
| qB |
| 60° |
| 360° |
| t1 |
| T1 |
粒子在Ⅱ区运动的周期:T2=
| 2πm |
| qB′ |
| 90° |
| 360° |
| t2 |
| T2 |
粒子在第一象限中运动的时间为:t=t1+t2 ⑧
联立⑤⑥⑦⑧解得:t=
| 7πm |
| 12qB |
(2)Q点坐标 x=OAcos30°+r2=r1cos30°+r2
代人数据得:x=
(
| ||
| 2qB |
故选:AC
点评:带电粒子通过磁场的边界时,如果边界是直线,根据圆的对称性得到,带电粒子入射速度方向与边界的夹角等于出射速度方向与边界的夹角,这在处理有界磁场的问题常常用到.

练习册系列答案
相关题目
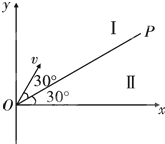 如图所示,在空间有一坐标系xoy,直线OP与x轴正方向的夹角为30°,第一象限内有两个方向都垂直纸面向外的匀强磁场区域Ⅰ和Ⅱ,直线OP是他们的边界,OP上方区域Ⅰ中磁场的磁感应强度为B.一质量为m,电荷量为q的质子(不计重力)以速度v从O点沿与OP成30°角的方向垂直磁场进入区域Ⅰ,质子先后通过磁场区域Ⅰ和Ⅱ后,恰好垂直打在x轴上的Q点(图中未画出),则( )
如图所示,在空间有一坐标系xoy,直线OP与x轴正方向的夹角为30°,第一象限内有两个方向都垂直纸面向外的匀强磁场区域Ⅰ和Ⅱ,直线OP是他们的边界,OP上方区域Ⅰ中磁场的磁感应强度为B.一质量为m,电荷量为q的质子(不计重力)以速度v从O点沿与OP成30°角的方向垂直磁场进入区域Ⅰ,质子先后通过磁场区域Ⅰ和Ⅱ后,恰好垂直打在x轴上的Q点(图中未画出),则( )A、粒子在区域Ⅰ中运动的时间为
| ||
B、粒子在区域Ⅰ中运动的时间为
| ||
C、粒子在区域Ⅱ中运动的时间为
| ||
D、粒子在区域Ⅱ中运动的时间为
|
 (2010?武汉二模)如图所示,在空间有一坐标系xoy,直线OP与x轴正方向的夹角为30°,第一象限内有两个方向都垂直纸面向外的匀强磁场区域I和II,直线OP是他们的边界,OP上方区域I中磁场的磁感应强度为B.一质量为m,电荷量为q的质子(不计重力)以速度v从O点沿与OP成30°角的方向垂直磁场进入区域I,质子先后通过磁场区域I和II后,恰好垂直打在x轴上的Q点(图中未画出),试求:
(2010?武汉二模)如图所示,在空间有一坐标系xoy,直线OP与x轴正方向的夹角为30°,第一象限内有两个方向都垂直纸面向外的匀强磁场区域I和II,直线OP是他们的边界,OP上方区域I中磁场的磁感应强度为B.一质量为m,电荷量为q的质子(不计重力)以速度v从O点沿与OP成30°角的方向垂直磁场进入区域I,质子先后通过磁场区域I和II后,恰好垂直打在x轴上的Q点(图中未画出),试求: ,第一象限内有两个方向都垂直纸面向外的匀强磁场区域Ⅰ和Ⅱ,直线OP是他们的边界,OP上方区域Ⅰ中磁场的磁感应强度为B。一质量为m,电荷量为q的质子(不计重力)以速度v从O点沿与OP成
,第一象限内有两个方向都垂直纸面向外的匀强磁场区域Ⅰ和Ⅱ,直线OP是他们的边界,OP上方区域Ⅰ中磁场的磁感应强度为B。一质量为m,电荷量为q的质子(不计重力)以速度v从O点沿与OP成



