题目内容
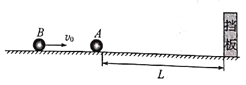
【题目】如图，足够大的光滑水平面上固定着一竖直挡板，挡板前L处静止着质量m1=1kg的小球A，质量m2=2kg的小球B以速度v0运动，与小球A正碰。两小球可看作质点，小球与小球及小球与挡板的碰撞时间忽略不计，且碰撞中均没有机械能损失。求
(1)第1次碰撞后两小球的速度；
(2)两小球第2次碰撞与第1次碰撞之间的时间；
(3)两小球发生第3次碰撞时的位置与挡板的距离。
【答案】(1)
方向均与
相同 (2)
(3)
【解析】
（1）第一次发生碰撞，动量守恒，机械能守恒；
（2）小球A与挡板碰后反弹，发生第2次碰撞，分析好位移关系即可求解；
（3）第2次碰撞过程中，动量守恒，机械能守恒，从而找出第三次碰撞前的初始条件，分析第2次碰后的速度关系，位移关系即可求解。
（1）设第1次碰撞后小球A的速度为
，小球B的速度为
，根据动量守恒定律和机械能守恒定律:
整理得：
，
解得
，
，方向均与相同。
（2）设经过时间
两小球发生第2次碰撞，小球A、B的路程分别为
、
，则有
，
由几何关系知：
整理得：
（3）两小球第2次碰撞时的位置与挡板的距离：
以向左为正方向，第2次碰前A的速度
，B的速度为
，如图所示。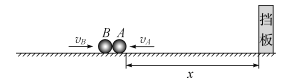
设碰后A的速度为
，B的速度为
。根据动量守恒定律和机械能守恒定律，有
； 
整理得：
，
解得：
，
设第2次碰后经过时间
发生第3次碰撞，碰撞时的位置与挡板相距
，则
，
整理得：
练习册系列答案
相关题目
