题目内容
如图3-2-3(1)所示,自空中相距d=5 cm的两块平行金属板A、B与电源连接(图中未画出),其中B板接地(电势为零),A板电势变化的规律如图(2)所示.将一质量m=2.0×10-27 kg,电量q=+1.6×10-19 C的带电粒子从紧临B板处释放,不计重力.求:
(1)在t=0时刻释放该带电粒子,释放瞬间粒子加速度的大小;
(2)若A板电势变化周期T=1.0×10-5 s,在t=0时将带电粒子从紧临B板处无初速释放,粒子到达A板时动量的大小;
(3)A板电势变化频率多大时,在t=![]() 到t=
到t=![]() 时间内从紧临B板处无初速释放该带电粒子,粒子不能到达A板?
时间内从紧临B板处无初速释放该带电粒子,粒子不能到达A板?

图3-2-3
解析:(1)电场强度E=![]()
带电粒子所受电场力F=qE=![]() ,F=ma
,F=ma
a=![]() =4.0×10-9m/s2
=4.0×10-9m/s2
(2)粒子在0—![]() 时间内走过的距离为
时间内走过的距离为![]() =5.0×10-2 m
=5.0×10-2 m
故带电粒子在t=![]() 时恰好到达A板根据动量定理,此时粒子动量p=Ft=4.0×10-23 kg·m/s
时恰好到达A板根据动量定理,此时粒子动量p=Ft=4.0×10-23 kg·m/s
(3)带电粒子在t=![]() —t=
—t=![]() 向A板做匀加速运动,在t=
向A板做匀加速运动,在t=![]() —t=
—t=![]() 向A板做匀减速运动,速度减为零后将返回.粒子向A板运动可能的最大位移s=2×
向A板做匀减速运动,速度减为零后将返回.粒子向A板运动可能的最大位移s=2×![]() =
=![]() aT2
aT2
要求粒子不能到达A板,有s<d
由f=![]() ,电势变化频率应满足f>
,电势变化频率应满足f>![]() ×104 Hz
×104 Hz
答案:(1)4.0×109 m/s2
(2)4.0×10-23 kg·m/s
(3)f>![]() ×104 Hz
×104 Hz

练习册系列答案
相关题目
在研究小车速度随时间变化规律的实验中,得到一条记录小车运动情况的点迹清晰的纸带,如图3-2-6所示,图中A、B、C、D、E为相邻计数点,相邻计数点的时间间隔T=0.1 s.
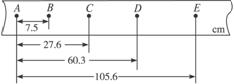
图3-2-6
(1)根据纸带上的数据,计算各点速度,填入下表中.
位置编号 | A | B | C | D | E |
时间t/s | 0 | 0.1 | 0.2 | 0.3 | 0.4 |
瞬时速度v/(m·s-1) |
|
|
|
|
|
(2)在图3-2-7中作出小车的v-t图线.

图3-2-7
 如图所示为一个固定在水平地面上的容器,容器上半部分为细筒,下半部分为粗筒,粗细筒的横截面积之比为3:1,且细筒足够长,上端与大气相通.已知外界大气压强为75cmHg,粗筒中有一个质量不计的活塞A,活塞的下方封闭一定质量的理想气体.当温度为27°C时,气柱长L=15cm,活塞A上方的水银柱高度H=5cm,水银柱上表面与粗筒上端相平,如图所示.活塞A的厚度及筒壁间的摩擦不计.试求:
如图所示为一个固定在水平地面上的容器,容器上半部分为细筒,下半部分为粗筒,粗细筒的横截面积之比为3:1,且细筒足够长,上端与大气相通.已知外界大气压强为75cmHg,粗筒中有一个质量不计的活塞A,活塞的下方封闭一定质量的理想气体.当温度为27°C时,气柱长L=15cm,活塞A上方的水银柱高度H=5cm,水银柱上表面与粗筒上端相平,如图所示.活塞A的厚度及筒壁间的摩擦不计.试求:
