题目内容
在水平面上有一沿y轴放置的长为L=1m的细玻璃管,在管底有光滑绝缘的带正电的小球,在第一象限中存在磁感应强度为B=1T的匀强磁场,方向如图所示,已知管沿x轴以v=1m/s的速度平动,带电小球的荷质比为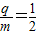 ,下列说法正确的是( )
,下列说法正确的是( )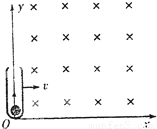
A.小球离开玻璃管前做变加速曲线运动
B.小球离开玻璃管的速度为
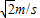 ,方向与x轴夹角为45°
,方向与x轴夹角为45°C.小球在磁场中做圆周运动的时间为
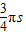
D.小球离开玻璃管的位置距离O点的距离为
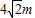
【答案】分析:对小球进行受力分析,根据牛顿第二定律求出小球的加速度,再利用运动学公式进行求解.
解答:解:A:小球相对于管子只能上下运动,所以不是类平抛运动,做变加速曲线运动.故A正确.
B:对小球受力沿管子方向分析如图:
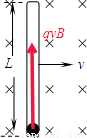 F合=qvB,由牛顿第二定律F合=ma得:
F合=qvB,由牛顿第二定律F合=ma得:
a=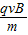 ;
;
由v2-v2=2al得:
v1=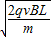 =1m/s;
=1m/s;
此时垂直于管子方向的速度为:v
所以离开时的速度为: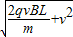 =
=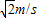 ,而方向与x轴夹角为45°,故B正确.
,而方向与x轴夹角为45°,故B正确.
C:小球在磁场中不做圆周运动,故C错误.
D:由:L= at2得:
at2得:
L=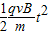
得:t=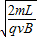 =2s.则x方向的位移为2m,所以小球离开玻璃管口距离O点的距离为
=2s.则x方向的位移为2m,所以小球离开玻璃管口距离O点的距离为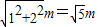 ,故D错误.
,故D错误.
故选:AB
点评:小球的合运动是沿管子方向的匀加速运动和垂直于管子方向的匀速直线运动的合运动,从两个方向分别分析即可..
解答:解:A:小球相对于管子只能上下运动,所以不是类平抛运动,做变加速曲线运动.故A正确.
B:对小球受力沿管子方向分析如图:
 F合=qvB,由牛顿第二定律F合=ma得:
F合=qvB,由牛顿第二定律F合=ma得:a=
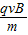 ;
;由v2-v2=2al得:
v1=
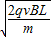 =1m/s;
=1m/s;此时垂直于管子方向的速度为:v
所以离开时的速度为:
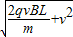 =
=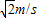 ,而方向与x轴夹角为45°,故B正确.
,而方向与x轴夹角为45°,故B正确.C:小球在磁场中不做圆周运动,故C错误.
D:由:L=
 at2得:
at2得:L=
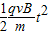
得:t=
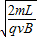 =2s.则x方向的位移为2m,所以小球离开玻璃管口距离O点的距离为
=2s.则x方向的位移为2m,所以小球离开玻璃管口距离O点的距离为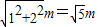 ,故D错误.
,故D错误.故选:AB
点评:小球的合运动是沿管子方向的匀加速运动和垂直于管子方向的匀速直线运动的合运动,从两个方向分别分析即可..

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案
相关题目
 在水平面上有一沿y轴放置的长为L=1m的细玻璃管,在管底有光滑绝缘的带正电的小球,在第一象限中存在磁感应强度为B=1T的匀强磁场,方向如图所示,已知管沿x轴以v=1m/s的速度平动,带电小球的荷质比为
在水平面上有一沿y轴放置的长为L=1m的细玻璃管,在管底有光滑绝缘的带正电的小球,在第一象限中存在磁感应强度为B=1T的匀强磁场,方向如图所示,已知管沿x轴以v=1m/s的速度平动,带电小球的荷质比为 在水平面上有一沿y轴放置的长为L=1m的细玻璃管,在管底有光滑绝缘的带正电的小球.在第一象限中存在磁感应强度为B=1T的匀强磁场,方向如图所示.已知管沿x轴以v=1m/s的速度平动,带电小球的荷质比为
在水平面上有一沿y轴放置的长为L=1m的细玻璃管,在管底有光滑绝缘的带正电的小球.在第一象限中存在磁感应强度为B=1T的匀强磁场,方向如图所示.已知管沿x轴以v=1m/s的速度平动,带电小球的荷质比为

